笔记之算法与数据结构（持续更新中）

笔记之算法和数据结构

面试需要掌握的算法与数据结构这一块的内容，大概有以下几点：

1. ​ 数组、链表、二叉树、队列、栈的各种操作（性能，场景）
2. ​ 二分查找和各种变种的二分查找
3. ​ 各类排序算法以及复杂度分析（快排、归并、堆）
4. ​ 各类算法题（手写）
5. ​ 理解并可以分析时间和空间复杂度。
6. ​ 动态规划（笔试回回有。。）、贪心。
7. ​ 红黑树、AVL树、Hash树、Tire树、B树、B+树。
8. ​ 图算法（比较少，也就两个最短路径算法理解吧）

分析时间复杂度

时间复杂度表示代码执行时间随数据规模增长的变化趋势。以下两个程序为例子

int cal(int n) { 
    int sum = 0;   
    int i = 1;  
    for (; i <= n; ++i) {  
        sum = sum + i;   
    }  
    return sum;
}

假设每段代码执行的时间都一样，记为 unit_time ，第二、第三行的代码都需要 1 unit_time，第四第五行都需要 n * unit_time ，那么这段代码的总执行时间就为 (2n+2)unit_time

PS：T(n) 代表的是代码的执行时间，n 表示数据规模的大小。f（n）表示每行代码执行的次数总和
如果用大 O 复杂度表示呢，就是 T( n )=O（f（n）），当 n 很大的时候，你可以将它想象为10000。而公式中的低阶、常量、系数三部分并不左右增长趋势，所以可以将它忽略。这段代码的时间复杂度就为 T(n) = O(n)

依次类推，再来分析下面这一段代码的时间复杂度

 int cal(int n) {   
     int sum = 0;
     int i = 1;
     int j = 1;
     for (; i <= n; ++i) { 
         j = 1; 
         for (; j <= n; ++j) { 
             sum = sum +  i * j;     
         }  
     }
 }

如果用大O复杂度表示呢，就是 T(n)=O(n)

假设每段代码执行的时间都一样，记为 unit_time ，第一、二、第三行的代码都需要 1 unit_time，第四、五行都需要 n * unit_time ，第六、七行都需要 n * n unit_time，所以总结起来，这段代码的总执行时间为（3+2n+2n²）n * unit_time
时间复杂度为：T(n) = O(n²)

方法和技巧

• 只关注循环次数最多的那一段代码。
  就拿上面的那段程序来讲吧，就是 时间复杂度为 O(n²)

• 加法法则：总复杂度等于量级最大的那段代码的复杂度

• int cal(int n) {
      //这一段能明显看出，它没有时间复杂度，哪怕循环体里面是10000也好，这是一个常量的执行时间，尽管它对程序的执行时间会有很大影响，但它对增长趋势并没有影响（时间复杂度的概念），所以呢，与时间复杂度无关，它的时间复杂度为 O(1)
      int sum_1 = 0;
      int p = 1;
      for (; p < 100; ++p) {
          sum_1 = sum_1 + p;   
      } 
  
      //这一段代码，明显就可以看出是 O(n)
      int sum_2 = 0;
      int q = 1;
      for (; q < n; ++q) {
          sum_2 = sum_2 + q;
      }
  
      //这一段代码，也可以轻易的看出时间复杂度为O(n²)
      int sum_3 = 0; 
      int i = 1;
      int j = 1;
      for (; i <= n; ++i) {
          j = 1;
          for (; j <= n; ++j) { 
              sum_3 = sum_3 +  i * j;
          }
      }
      return sum_1 + sum_2 + sum_3; 
  } 

  那么根据加法法则：T1(n) = O(f(n))，T2(n) = O(g(n))；那么T(n)=T1(n) + T2(n) = max(O(f(n))，O(g(n))) = max((f(n)，g(n))

• 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

• //可以简单的一眼看出，这段代码的时间复杂度为 O(n)
  int cal(int n) {
      int ret = 0;
      int i = 1;
      for (; i < n; ++i) {
          ret = ret + f(i);
      } 
  } 
  //这段代码的时间复杂度也同样为 O(n)
    int f(int n) { 
        int sum = 0;
        int i = 1;
        for (; i < n; ++i) {
            sum = sum + i;
        }
        return sum; 
    }

• 因为第一段程序的循环体里面包含了，第二段程序的运行，所以它们嵌套了。
  T(n) = T1(n) * T2(n) = O(n*n) = O(n²)

常见的时间复杂度量级

常量阶 O(1)	线性阶 O(n)	平方阶 O（n²）
对数阶 O(Log n)	线性队数阶 O(nLog n)	立方阶 O(n³)
指数阶 O(2^n)	阶乘 O(n!)	k 次方阶 O(n^k)

• O(1)
  只要代码的执行时间不随着 n 的增大而增长，那么这样的事件复杂度就为 O(1)。
  只要算法中不存在循环语句（涉及到 n 之类的）、递归语 句，即使有成千上万行的代码，其时间复杂度也是Ο(1)。

• O(logn)、O(n log n)

• 对数阶时间复杂度非常常见，同时也是最难分析的一种时间复杂度。

• i=1;
  while (i <= n)  { 
      i = i * 2; 
  }

• 类似于一个等比数列，2^0 * 2^1 * 2^2 * ….. 2^k * …… 2^x = n
  只要知道 X 的值是多少，就可以知道这行代码的执行粗疏，通过 2^x = n。
  x=log2n （2是底数，不知道为什么输入不出来）O(log2n)

• 根据上面的这个例子，来观察下面这个程序

• i=1;
  while (i <= n)  { 
      i = i * 3; 
  }

• 类似于一个等比数列，3^0 * 3^1 * 3^2 * ….. 3^k * …… 3^x = n
  时间复杂度也类似的，x=log3n。O(log3n)

• 对数之间是可以相互转换的，在采用 大O 标记复杂度的时候，可以忽略系数，即O(Cf(n)) = O(f(n))。所以上面两段代码的时间复杂度都可以为 O(logn)。

• O(nlogn)就是基于乘法法则的，如果一段代码的时间复杂度为 log(longn)，那么循环执行 n 遍，时间复杂度就是 O（nlogn），比如，归并排序、快速排序的时间复杂度都是 O(nlogn)

• O（m+n）、O(m*n)

• int cal(int m, int n) {
      int sum_1 = 0;
      int i = 1;
      for (; i < m; ++i) {
          sum_1 = sum_1 + i;
      }  
      int sum_2 = 0;
      int j = 1;
      for (; j < n; ++j) { 
          sum_2 = sum_2 + j;
      }
      return sum_1 + sum_2;
  } 

• 从代码中看出，这个 cal 函数里有 m 和 n 两个数据规模，无法判断 m 和 n 的量级大，所以在表示复杂度时，就不要简单的用加法法则，上面的时间复杂度是 O(m+n)

• 所以这种情况，我们需要将加法法则改为 T1(m) + T2(n) = O(F(m) + g(n))。
  但是乘法法则继续有效： T1(m)*T2(n) = O(f(m) * f(n))

空间复杂度分析

• 时间复杂度的全称是渐进时间复杂度，表示算法的执行时间与数据规模之间的关系。同理，空间复杂度的全称是渐进空间复杂度，表示算法的存储空间与数据规模之间的增长关系。

• 以以下的代码为例子：

• void print(int n) {
      int i = 0;
      int[] a = new int[n];
      for (i; i < n; ++i) {
          a[i] = i * i;
      }
      for (i = n-1; i >= 0; --i) {
          print out a[i]  
      } 
  }

• 和时间复杂度分析一样，第二行代码，我们申请了一个空间存储变量 i，但它是常量阶的，跟数据规模 n 没有关系，忽略不计。那么第三行代码，申请了一个大小为 n 的 int 类型数组，除此之外，剩下的代码都没有占用更多的空间，所以它的空间复杂度为 O（n）。

• 空间复杂度，指的是除了原本的数据存储空间外，算法运行时还需要的额外的存储空间

• 常见的空间复杂度为 ：O(1)、O(n)、O(n²)

数组

数组是一种线性表数据结构，使用连续的内存存储空间，存储一组相同类型数据

数组支持随机访问，根据下标随机访问的时间复杂度为 O(1)

数组的低效插入和低效删除

在数组的末尾插入元素，就不用移动数据，时间复杂度为 O(1)
在数组的开头插入元素，每个数组都要移动，最坏时间复杂度为 O(n)
在每个位置插入元素的概率一致，平均时间复杂度为 O(n)
删除和插入类似，时间、最坏、平均复杂度都一致

容器能否完全替代数组？

针对数组类型，很多语言都提供了容器类，比如 Java 中的 ArrayList
ArrayList 最大的优势就是可以将很多数组操作的细节封装起来。比如前面提到的数组插入、删除数据时需要搬移其他数据等。另外，它还有一个优 势，就是支持动态扩容。

1.Java ArrayList 无法存储基本类型，比如 int、long，需要封装为 Integer、Long类，而 Autoboxing、Unboxing 则有一定的性能消耗，所以如果特别关注性能，或者希 望使用基本类型，就可以选用数组。

2.如果数据大小事先已知，并且对数据的操作非常简单，用不到 ArrayList 提供的大部分方法，也可以直接使用数组。

3.当要表示多维数组时，用数组往往会更加直观。比如Object[][] array；而用容器的话则需要这样定义：ArrayList array。

链表

常见的三种链表结构：单链表、双向链表、循环链表

单链表

头结点记录链表的基址，尾结点指向 Null

单链表的插入和删除操作，时间复杂度为 O(1)，因为只需要考虑相邻结点的指针改变，链表的存储空间本身不是连续的

单链表的随机访问：因为存储空间不连续的，需要根据指针一个结点一个结点地依次遍历，直到找到相应的结点，时间复杂度为 O(n)

循环链表

尾结点指针指向链表的头结点
当处理的数据有环形结构特点时，适合用循环链表。比如著名的约瑟夫问题

双向链表

支持两个方向，每个结点不止一个后继指针 next 指向后面的结点，还有个前驱指针 prev 指向前面的结点

双向链表的插入和删除时间复杂度都为 O(1)，双向链表的插入和删除操作比单链表更简单、高效

比如：删除操作，从链表中删除一个数组，有两种情况：

• 删除结点中“值等于某个给定值”的结点
• 删除给定指针指向的结点

第一种情况：
无论是单链表还是双向链表，都要先从头开始遍历，直到找到“值等于给定值”的结点，然后再通过指针操作将其删除

删除操作时间复杂度是 O(1)，遍历查找是主要的耗时点，时间复杂度为 O(n)
根据上面讲过的加法法则，删除“值等于给定值”结点对应的链表操作的总时间复杂度为 O(n)

第二种情况：
找到要删除的结点后，删除某个结点 q 需要知道它的前驱结点，单链表并不支持直接获取前驱结点，所以要找到前驱结点，还是要从头结点开始遍历链表，找到 P->next = q ，说明 p 是 q 的前驱结点
对于双向链表而言，就不用这么复杂，找到结点后就知道它的前驱结点是谁，因为双向链表的结点中有保存前驱结点的指针

修改操作也是一样的，单向链表需要 O(n) 的时间复杂度，而循环链表只需要 O(1) 的时间复杂度，

对于有序链表，双向链表在查询时也有很大优势，在查询时，可以记录上次查询的位置 q ，每次查询，根据要查找的值与 p 的大小关系，决定往前还是往后查找，只需查询一半的数据

在实际开发中，双向链表虽然很费内存，但还是比单链表应用更广泛。java 语言的 LinkedHashMap 容器底层，就用到双向链表这种数据结构。

两个重要思想：

空间换时间的设计思想：当内存空间十分充足，如果追求代码的运行速度，就可以选择空间复杂度高，时间复杂度低的算法或者数据结构。

时间换空间的设计思想：内存比较紧缺，比如代码运行在手机或者单片机上。
就可以选择空间复杂度低，时间复杂度高的算法或者数据结构。

双向循环链表

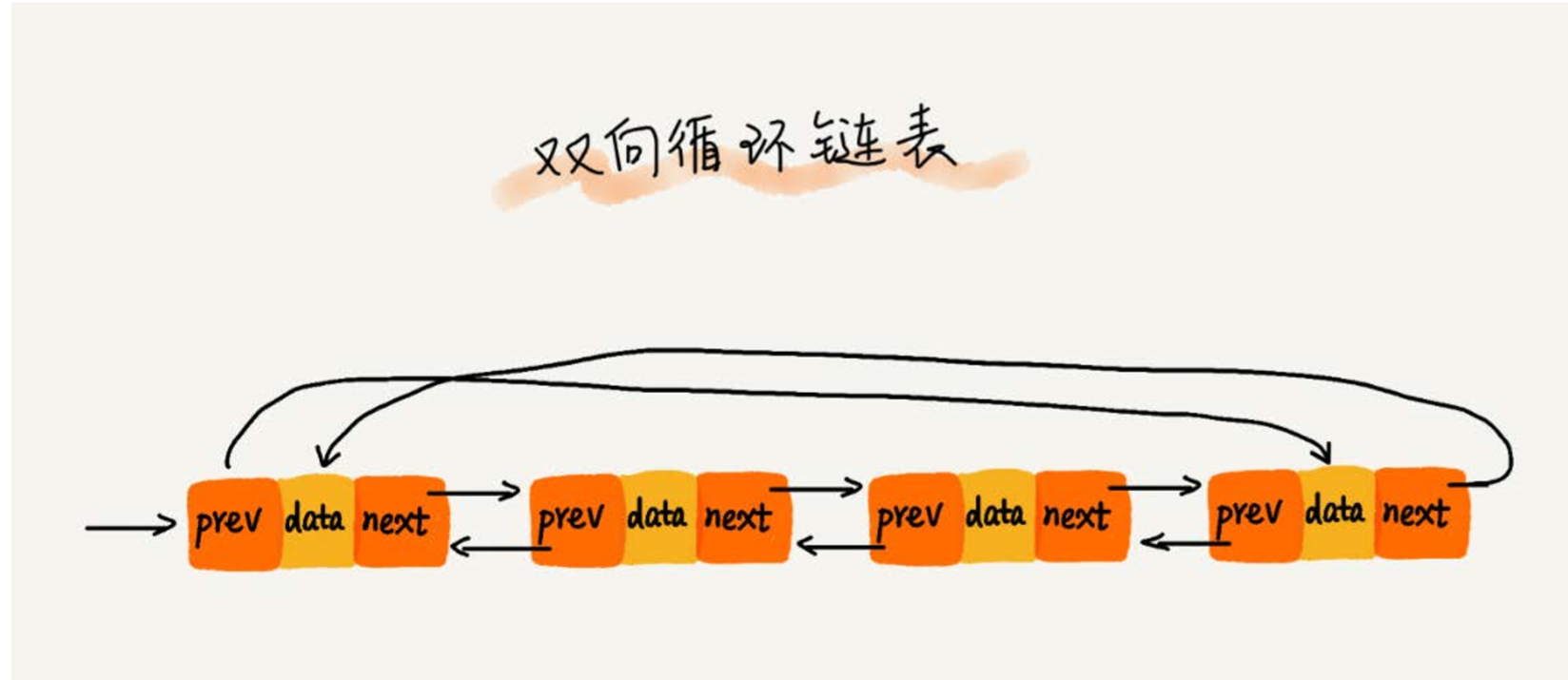
数组和链表的区别：

数组简单易用，实现上用的是连续的内存空间，可借助 CPU 的缓存机制，预读数组中的数据，访问效率高。
但链表在内存中并不是连续存储，对 CPU 缓存不友好，不能有效的预读

数组的缺点是大小固定，一经声明就要占用整块的连续内存空间。
声明的数组过大，系统没有足够的连续内存空间分配给它，导致内存不足。
声明的数组过小，不够用，只能申请一个更大的新的数组，进行数据拷贝，而数据拷贝是非常耗时的。
链表本身没有大小的限制，支持动态扩容。

如果代码对内存的使用苛刻，适合使用数组。

链表和指针容易混淆：

• 指针或引用的含义

  C 语言有指针的概念，Java 和 Python 没有指针，用引用来代替。实际上这些概念的意思都一样，都是存储所指对象的内存地址

  指针：将某个变量赋值给指针，相当于将这个变量的地址赋值给指针

  比如：p->next=q 意思就是 p 结点的 next 指针存储了 q 结点的内存地址

  p->next=p->next->next 意思就是 p 结点的 next 指针存储了下下个结点的内存地址

• 指针丢失和内存泄漏

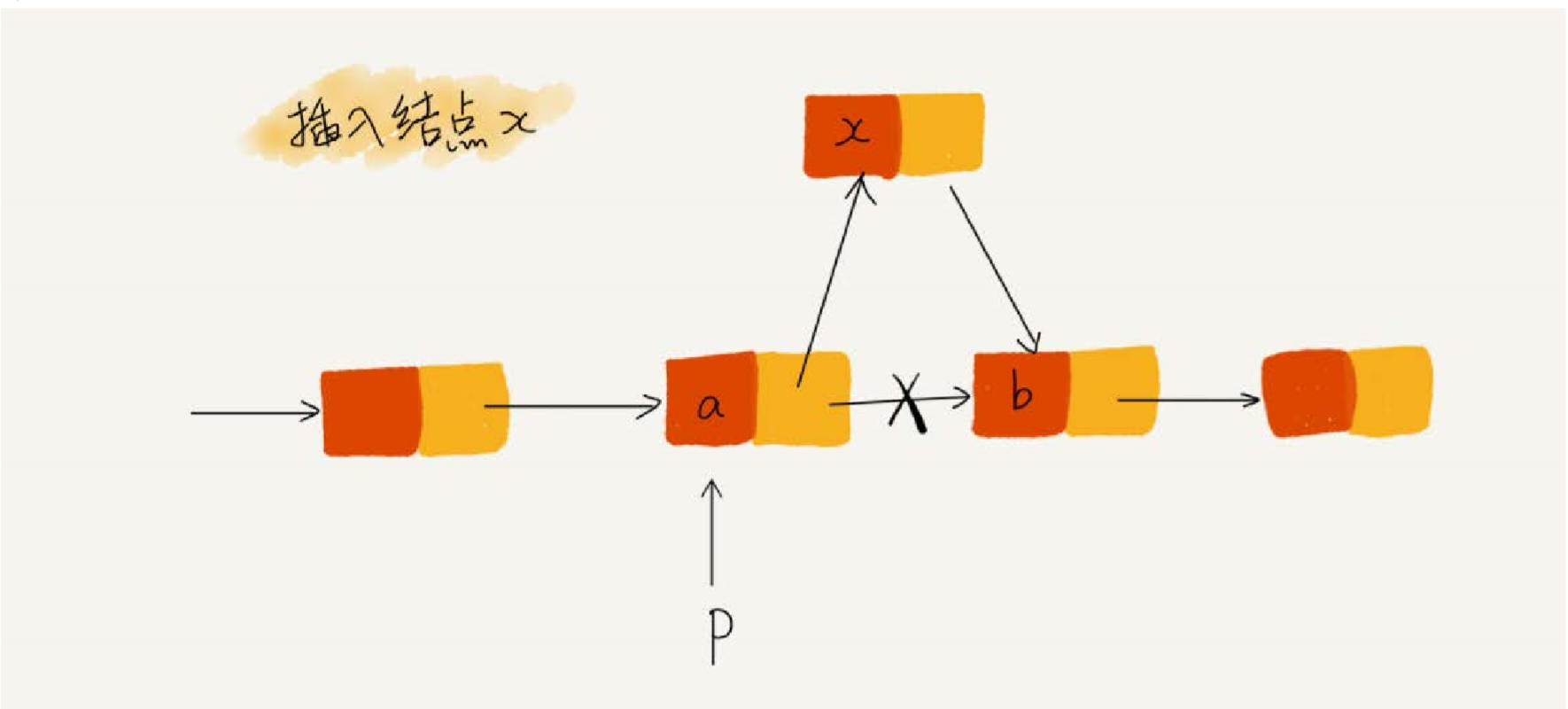
  x->next = p->next //将 x 结点的 next 指针指向 b 结点
  p->next = x       //将 p 的 next 指针指向 x 结点

如果顺序调转过来，就会发生指针丢失和内存泄漏

• 哨兵简化实现难度

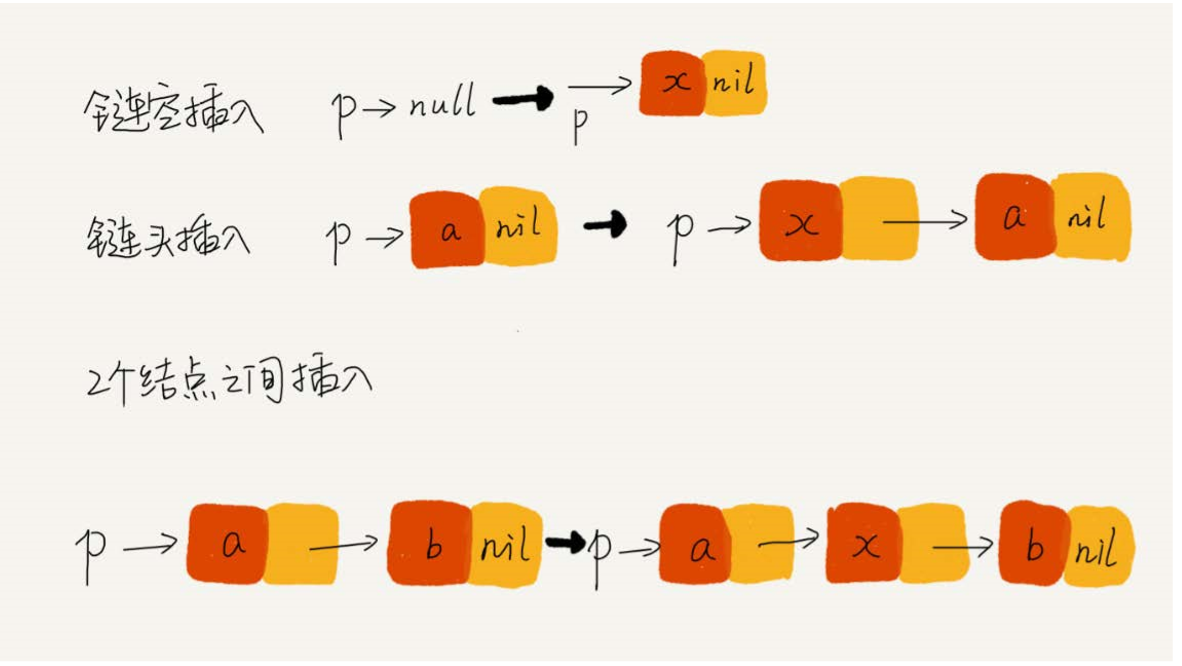
  ​ 单链表的插入：在结点 P 后面插入一个新的结点

  new_node -> next = p -> next
  p -> next = new_code

  ​ 但是是有条件的，如果在空链表中插入新结点，那么就是下面这种了

  if(head == null){
      head = new_code;
  }

  ​ 单链表的删除：删除结点 P 的后继结点

  p -> next = p -> next ->next

  ​ 假如删除链表中的最后一个结点，上面这段代码就行不通

  if(head -> next == null){
      head = null;
  }

  ​ 哨兵结点，是用来解决边界问题的，不直接参与业务逻辑

  ​ 在任何时候，不管链表是不是空， head 指针会一直指向哨兵结点， 这种带有哨兵结点的链表也叫做带头链表。没有哨兵结点的链表就叫做不带头链表

• 重点留意边界条件处理

  ​ 经常要检查链表代码是否正确的边界条件有：

  • 如果链表为空，代码是否能正常工作？

  • 如果链表只包含一个结点时，代码是否能正常运行？

    如果链表只包含两个结点时，代码是否能正常运行？

  • 代码逻辑在处理头结点和尾结点时，是否正常工作

    不光光是链表代码，任何代码都要考虑边界值或者异常情况

• 举例画图，辅助思考

  ​ 找一个具体的例子，把它画在纸上。比如单链表的插入

  

• 常见的链表操作

  • 单链表反转
  • 链表中环的检测
  • 两个有序的链表合并
  • 删除链表倒数第 n 个结点
  • 求链表的中间结点

栈

使用场景

• 众所周知，栈是一种“先进后出”的数据结构
• 从栈的操作特性上看，栈是一种“操作受限”的线性表，只能在一端插入和删除数据
• 在功能上，数组或链表确实可以替代栈，但是，特定的数据结构是对特定场景的抽象，数组和链表暴露了太多的操作接口，操作上确实灵活自由，但使用时较不可控
• 所以当某个数据集合只涉及在一端插入和删除数据，并且满足后进先出、先进后出的特性，首选“栈”这种数据结构

实现“栈”

• 栈可以使用用数组或链表实现，数组实现的栈叫顺序栈，链表实现的栈叫链式栈
• 入栈和出栈的实现

    public class ArrayStack {
        private String[] items; //数组
        private int count;  //栈中元素个数
        private int n;  //栈的大小

        //初始化数组，申请一个大小为 n 的数组空间
        public ArrayStack(int n){
            this.items = new String[n];
            this.count = 0;
            this.n = n;
        }

        //入栈操作
        public boolean push(String item) {
            //数组空间不够了，直接返回 false , 而且 count + 1
            if (count == n){
                return false;
            }
            items[count] = item;
            ++count;
            return true;
        }

        //出栈操作
        public String pop(){
            //栈为空，则直接返回 null
            if (count == 0){
                return null;
            }

            //返回下标为 count-1 的数组元素，并且栈中元素个数 count-1
            String tmp = items[count - 1];
            --count;

            return tmp;
        }
    }

时间和空间复杂度的计算

• 不管时顺序栈还是链式栈，存储数据只要一个大小为 n 的数组。入栈和出栈的过程，临时变量存储空间只用一两个，空间复杂度即为 O(1)

  为什么存储数据用了大小为 n 的数组，空间复杂度不是 O（n）?

  因为 n 这个空间是必须的，不能省掉，所以说空间复杂度，指的是除了原本的数据存储空间外，算法运行时还需要的额外的存储空间

• 时间复杂度的分析，因为入栈和出栈只是涉及到栈顶个别数组的操作，所以时间复杂度为 O(1)

支持动态扩容的顺序栈

• 想要支持动态扩容的栈，只要底层依赖一个支持动态扩容的数组。栈满之后，就申请一个更大的数组，将原来的数据搬到新数组中。

• 分析动态扩容的顺序栈的入栈、出栈操作时间复杂度

  出栈时，不会涉及到内存的重新申请和数据搬移，出栈的时间复杂度时O(1)。
  而入栈的时间复杂度分两种情况

  ​ 在栈的空间充足时，入栈操作的时间复杂度为O(1)。
  ​ 在栈的空间不足时，需要重新申请内存和数据搬移，时间复杂度就变成了O(n)

  对于入栈操作，最好的时间复杂度是O(1)，最坏的时间复杂度为 O(n)。平均复杂度为O(1)

栈在函数调用中的应用

• 栈的应用场景：函数调用栈

  操作系统给每一个线程分配了一块独立内存空间，这内存被称为“栈”这种结构，用来存储函数调用时的临时变量

  每进入一个函数，就会将临时变量作为一个栈帧入栈，被调用函数执行完成后，返回之后，这个函数对应的栈帧出栈。

  int main() {
   int a = 1;
   int ret = 0;
   int res = 0;
   ret = add(3, 5);
   res = a + ret;
   printf("%d", res);
   reuturn 0;
  }
  int add(int x, int y) {
   int sum = 0;
   sum = x + y;
   return sum;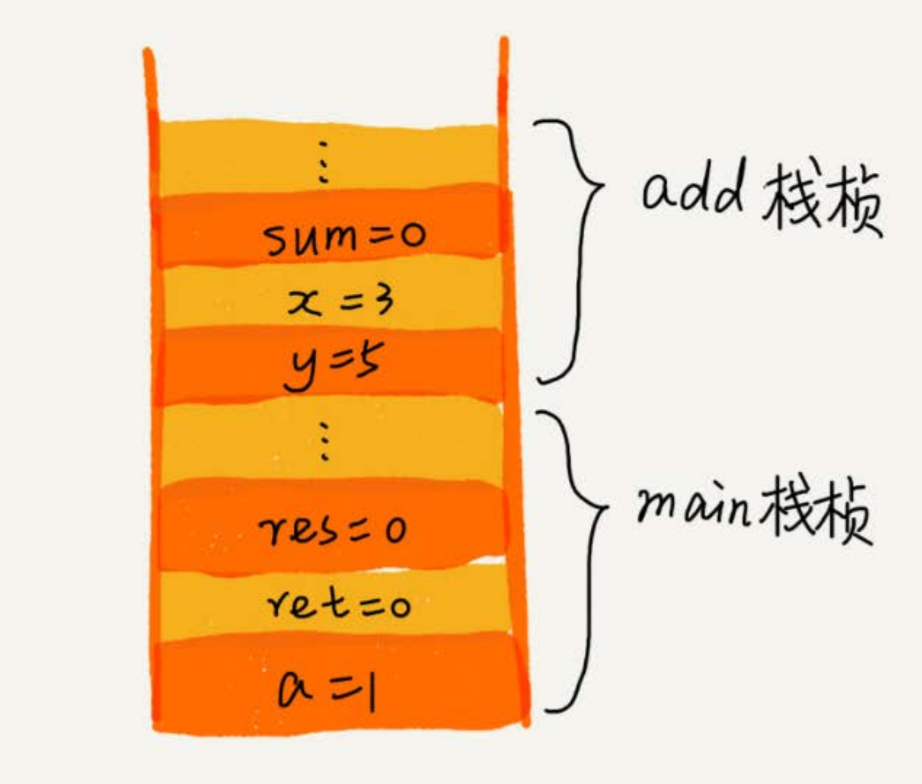
  }

  

栈在表达式求值中的应用

• 编译器如何利用栈来实现表达式求值

  比如 3+5*8-6 这个表达式，要通过两个栈区实现，其中一个栈保存操作数，一个栈保存运算符。
  从左往右遍历表达式，遇到数字，压入操作数栈。
  遇到运算符，就与运算符栈的栈顶元素比较。如果比运算符栈顶元素的优先级高，就将当前运算符栈压入栈，如果比运算符栈顶元素的优先级低或者相同，从运算符栈中取栈顶运算符，从操作数栈顶取两个操作数，进行计算，再把计算完的结果压入操作数栈，继续比较。图解形式理解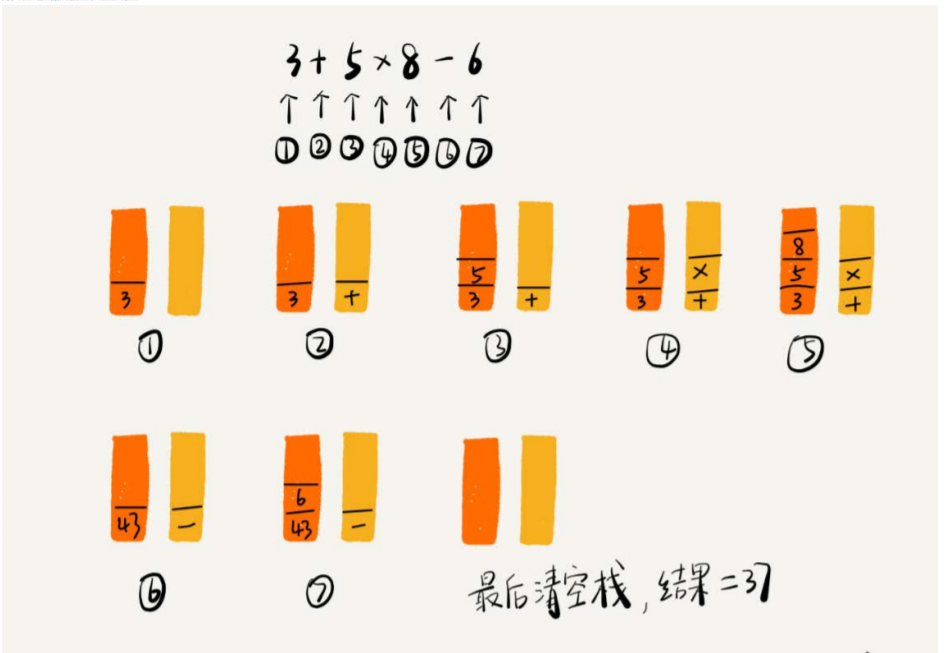

  

栈在括号匹配中的运用

• 假设表达式中只包含三种括号，圆括号()、方括号[]、花括号{}，并且可以任意嵌套。比如， {[{}]}或[{()}([])]等都为合法格式， ， {[}()]或[({)]为不合法的格式 ，检查是否合法

  用栈保存未匹配的左括号，从左到右依次扫描字符串。当扫描到左括号时，则将其压入栈中。当扫描到右括号时，从栈顶取出一个左括号。如果能匹配，比如 “(”跟“)”匹配，“[”跟“]”匹配，“{”跟“}”匹配 ，继续扫描剩下的字符串，遇到不能匹配的，或者栈中没有这个数据，则为非法格式

队列

队列的作用与应用

• 有循环队列、阻塞队列、并发队列等等
• 在偏底层系统、框架、中间件的开发中，有着关键性作用。
• 比如高性能队列 Disruptor、Linux 环形缓存，都用到了循环并发队列； java concurrent 并发包利用 ArrayBlockingQueue 来实现公平锁

顺序队列

• 队列和栈一样，队列可以用数组来实现（顺序队列），也可以用链表实现（链式队列）

• 基于数组的实现方法

   //用数组实现的队列
       public class ArrayQueue {
          //数组：items，数组大小：n
          private String[] items;
          private int n = 0;
          //head 表示队头下标，tail 表示队尾下标
          private int head = 0;
          private int tail = 0;
          //申请一个大小为 capacity 的数组
       public ArrayQueue(int capacity) {
          items = new String[capacity];
          n = capacity;
       }
       //入队
       public boolean enqueue(String item) {
       //如果tail == n 表示队列已经满了
           if (tail == n) {
               return false;
           }
           items[tail] = item;
           ++tail;
           return true;
       }
          // 出队
           public String dequeue() {
           // 如果head == tail 表示队列为空
               if (head == tail)
                   return null;
               // 把--操作放到单独一行来写
                 String ret = items[head];
                 ++head;
                 return ret;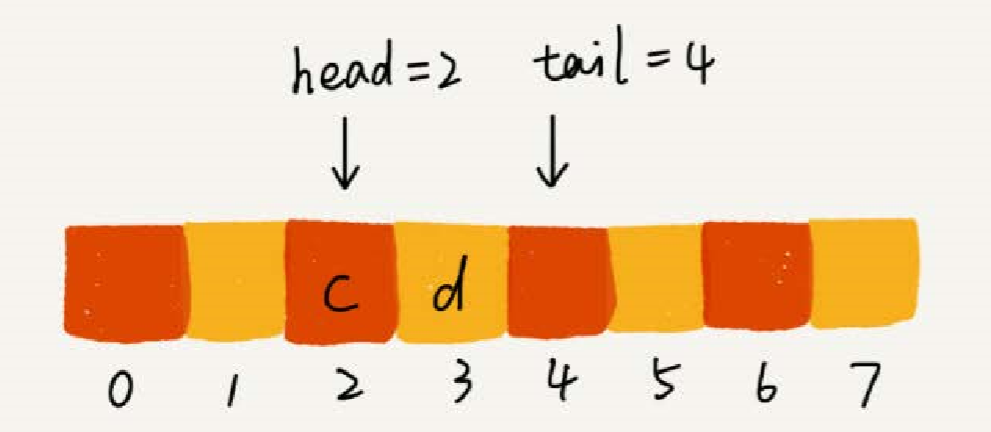
       }
       }

  

  随着不停的入队、出队的操作，head 和 tail 都会持续往后移动。当 tail 移动到最后边，即便数组中还有空闲空间，也无法继续往数组中添加数据。

  解决的办法：在出队时不用搬移数据，入队时，集中触发一次的数据搬移操作。出队函数 dequeue() 保持不变，修改入队函数 enqueue() 的实现

     //优化后的入队
           public boolean enqueue(String item){
           if (tail == n){
               if (head == 0){
                   return false;
               }
               for (int i = head; i < tail; ++i){
                   items[i-head] = items[i];
               }
               tail = tail - head;
               head = 0;
           }
           items[tail] = item;
           ++tail;
           return true;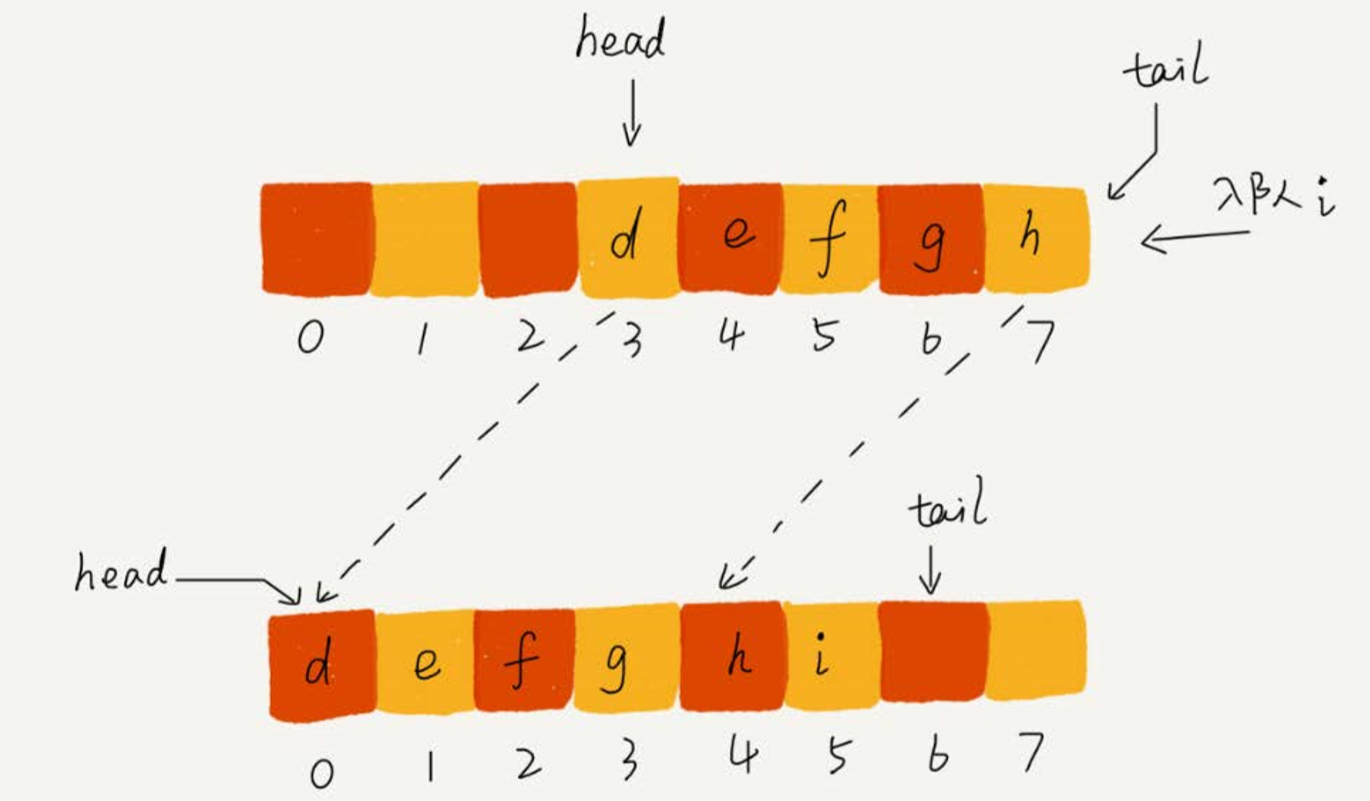
          }

  

链式队列

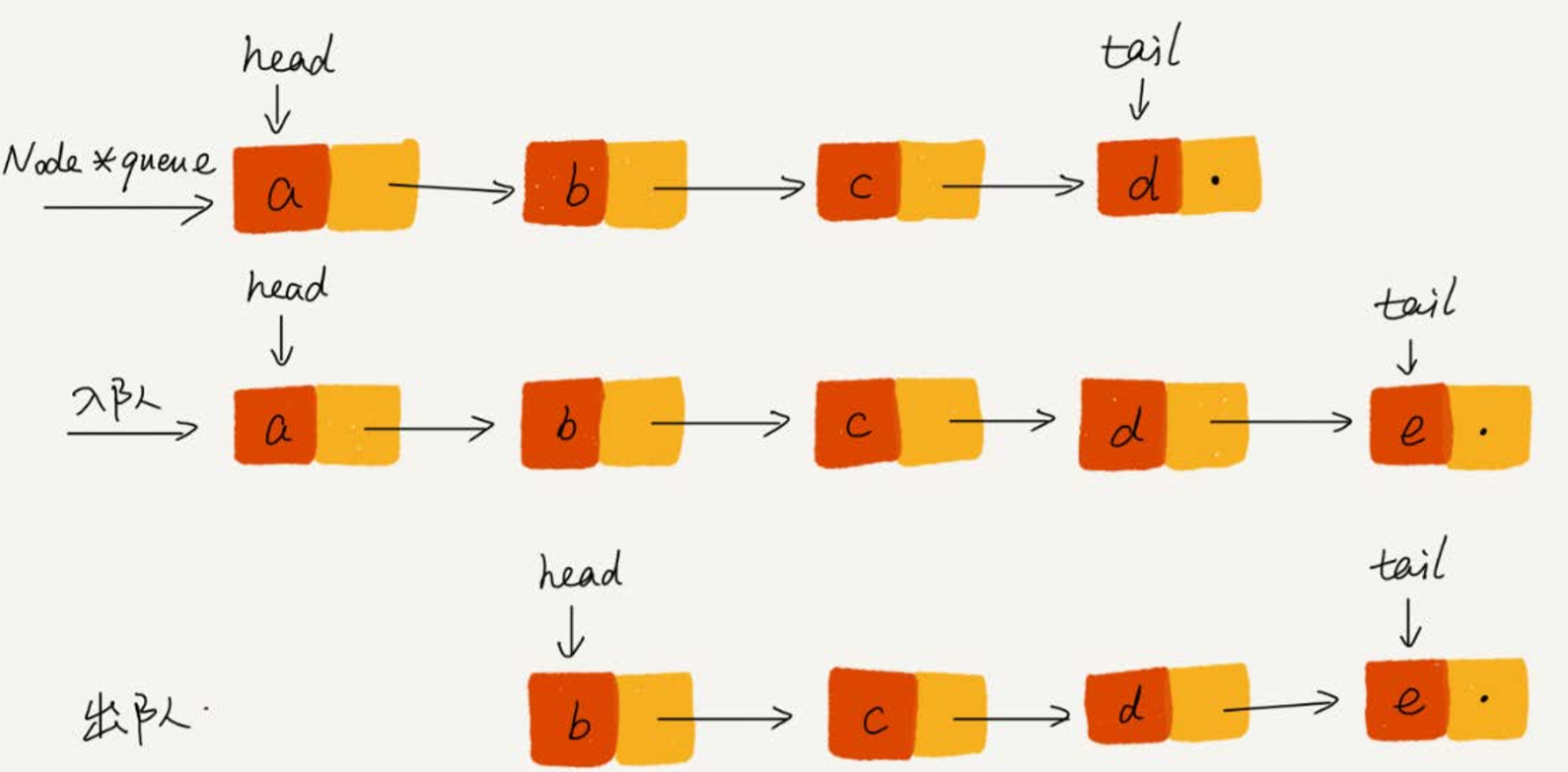
链表的实现，需要两个指针，head 指针和 tail 指针。分别指向链表的第一个结点和最后一个结点。

入队时的操作：tail -> next = new_code , tail = tail -> next
出队时的操作：head = head -> next

循环队列

循环队列避免了用数组实现队列的适合，在 tail == n 时的数据搬移操作

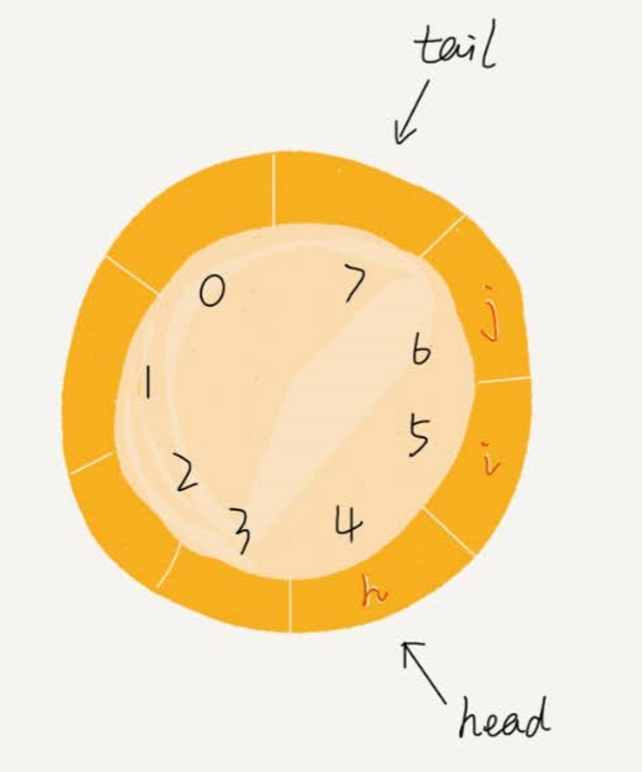
当插入一个新元素的时候，tail 更新为 下标为 0 的位置

队列为空的判断条件： head = tail
队列满的判断条件： (tail+1)%n = head

  public class CircularQueue {  
      // 数组：items，数组大小：n  
         private String[] items;  
           private int n = 0;
        // head 表示队头下标，tail 表示队尾下标  
         private int head = 0;  
         private int tail = 0;  
         // 申请一个大小为 capacity 的数组  
         public CircularQueue(int capacity) {    
             items = new String[capacity];    
             n = capacity;  
         }  
         // 入队  
         public boolean enqueue(String item) {
             // 队列满了    
              if ((tail + 1) % n == head) 
                  return false;    
              items[tail] = item;
              tail = (tail + 1) % n;
              return true;
         }  
         // 出队  
         public String dequeue() { 
             // 如果head == tail 表示队列为空
                 if (head == tail) 
                     return null; 
                 String ret = items[head]; 
                 head = (head + 1) % n; 
                 return ret;  
         } 
    }

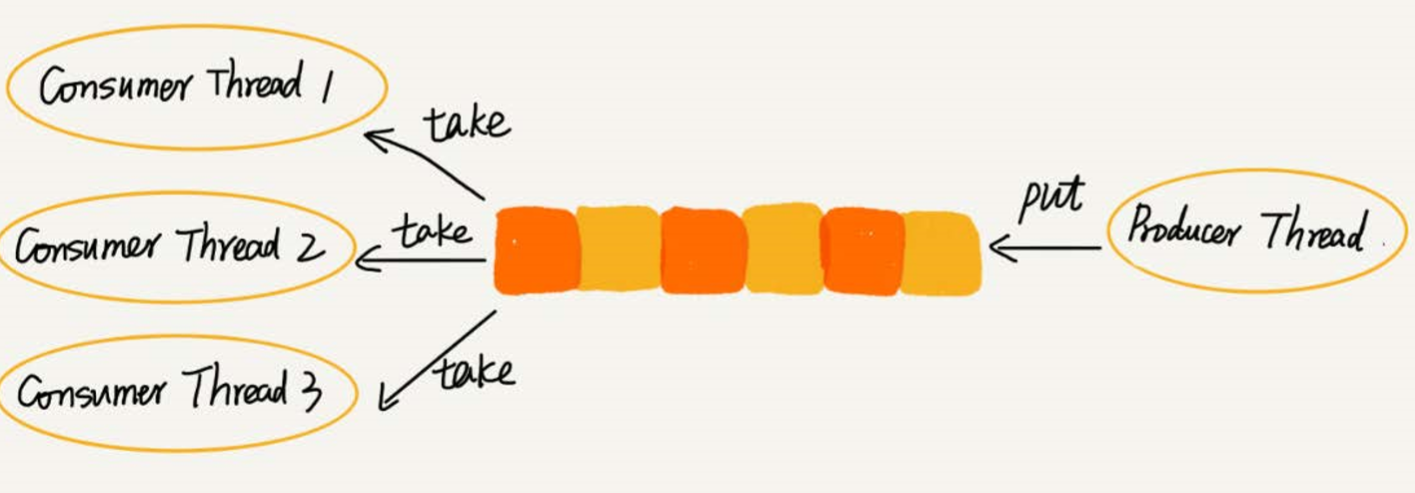
阻塞队列

队列为空时，从队头取数据会阻塞，除非队列有数据后才返回

如果队列满了，那么插入数据的操作会被阻塞，直到队列有空闲后再插入数据，再返回

这是一个“生产者——消费者模型”，当“生产者”产生数据的速度太快，可以调度多几个“消费者”

并发队列

线程安全的队列叫做并发队列，最简单直接的实现方式时直接在 enqueue()、dequeue() 方式上加锁，锁粒度大并发度较低，同一时刻仅允许一个存在者取操作。基于数组的循环队列，采用 CAS 原子操作，可实现高效的并发队列

递归

简单的例子理解递归概念

周末你带着女朋友去电影院看电影，女朋友问你，咱们现在坐在第几排啊？电影院里面太黑了，看不清，没法数，现在你怎么办？ 别忘了你是程序员，这个可难不倒你，递归就开始排上用场了。

于是你就问前面一排的人他是第几排，你想只要在他的数字上加一，就知道自己在哪一排了。但是，前面的人也看不清啊，所以他也问他前面的人。就这样一排一排往前问，直到问到第一排的人，说我在第一排，然后再这样一排一排再把数字传回来。直到你前面的人告诉你他在哪一排，于是你就知道答案了。 这就是一个非常标准的递归求解问题的分解过程，去的过程叫“递”，回来的过程叫“归”。

基本上，所有的递归问题都可以用递推公式来表示。刚刚这个生活中的例 子，我们用递推公式将它表示出来就是这样的 ： f(n)=f(n-1)+1 其中，f(1)=1

int f(int n) {
    if(n == 1){
        return 1;
    }
    return f(n-1) + 1;
}

递归要满足的三个条件

• 一个问题的解可以分解成几个子问题的解
  子问题就是数据规模更小的问题，比如电影院里，相对于“我在哪一排”，“我前面一排的人在哪一排”就是个数据规模更小的问题，

• 问题与分解之后的子问题，除了数据规模不同，求解思路完全一样

  还是以电影院举例子，问题是“我在哪一排”，分解之后的子问题是“前面一排的人在哪一排”，求解思路一样

• 存在递归终止条件

  子问题不能无限循环下去，电影院的例子，递归的终止条件就是，第一排的人知道自己在第一排，f(1) = 1;

编写递归代码

步骤：写出递推公式 ——> 找到终止条件，将递推公式转化代码

题目： 假如这里有n个台阶，每次你可以跨1个台阶或者2个台阶，请问走这n个台阶有多少种走法？

思路：根据第一步走的台阶进行分类，第一类是第一步走了一个台阶，
第二类就是第一步走了两个台阶。n 个台阶的走法就等于先走 1 阶后，n-1 个台阶的走法加上先走 2 阶后 n-2 个台阶的走法。
即是： f(n) = f(n-1) + f(n-2)

接下来就是找到终止条件，什么情况下不用递归了？
很明显，当只有一个台阶时，就没必要去递归了。担心递归条件不够充足，那就可以用 n=2，n=3 试验一下。
当 n = 2 时，f(2) = f(1) + f(0)。但 f(0) 显得不符合逻辑思维。

所以递归的终止条件是 f(1) = 1，f(2) = 2

总结一下：
f(1) = 1；
f(2) = 2；
f(n) = f(n-1) + f(n-2)；

if(n == 1) return 1;
if(n == 2) return 2;
return f(n - 1) + f(n - 2);

递归代码要警惕堆栈溢出

堆栈溢出，会造成系统性崩溃，后果很严重

对于栈，函数调用会使用栈来保存临时变量。每调用一个函数，会将临时变量封装栈帧压入内存栈，等函数执行完成返回时，出栈。
系统栈或者虚拟机栈空间一般不大，如果递归求解的数据规模很大，调用层数很深，一直压入栈，会有堆栈溢出的风险。

如何避免堆栈溢出：通过代码中限制递归调用的最大深度的方式来解决，给定一个深度界限，比如递归调用超过一定深度后，就不继续向下递归，而是直接抛出异常

递归代码要警惕重复计算

假如这里有n个台阶，每次你可以跨1个台阶或者2个台阶，请问走这n个台阶有多少种走法？

if(n == 1) return 1;
if(n == 2) return 2;
return f(n - 1) + f(n - 2);

上面这段代码，明显有重复计算的累赘性

想要避免这种情况，通过一个数据结构来保存，已经求解过的 f(k) 。

当递归调用到 f(k) ，从数据结构中看下，是否已经计算过这个值，若有，直接调用
改造后：

public int f(int n) {
    if(n == 1) return 1;
    if(n == 2) return 2;
    if(hasSolveList.containsKey(n)){
        return hasSolveList.get(n);
    }
    int ret = f(n - 1) + f(n + 1);
    hasSolveList.put(n,ret);
    return ret;
}

在时间效率上，递归代码上多了函数调用，当函数调用的数量很大，时间成本会很高。
空间复杂度，因为递归每调用一次就会在内存栈中保存一次现场数据，所以分析递归代码空间复杂度，需要额外考虑这部分，电影院递归代码，空间复杂度不是 O(1)，而是 O(n)。

将递归代码改写成非递归代码

递归代码：表达力强，简洁。
但是空间复杂度高，有栈堆溢出的风险，有重复计算、过多的函数调用会耗时多等问题。

电影院的例子改成非递归的代码

int f(int n){
    int ref = 1
    for(int i = 2; i <= n; ++i){
        ref = ref + 1;
    }
    return ref;
}

第二个例子也可以改成非递归的实现方式：

public int f(int n) {
    if(n == 1) return 1;
    if(n == 2) return 2;

    int ref = 0;
    int before = 2;
    int beforebefore = 1;
    for(int i = 3; i <= n; ++i){
        ref =  before + beforebefore;
        beforebefore = before;
        before = ref;
    }
    return ref;
}

所有递归代码都可以改玮这种迭代循环的非递归写法，递归本身是借助栈实现的，但是这种思路只是将递归变成了“手动递归”，本质没变，徒增实现复杂度

排序

排序算法执行效率

从以下几方面分析

• 最好情况、最坏情况、平均时间复杂度

  有些排序算法会进行区分；

  对于要排序的数据，有的接近无序，有的接近有序，有的完全无序

• 时间复杂度的系数、常数、低阶

  时间复杂度反应的是数据规模 n 很大的时候，可以忽略系数、常数、低阶，但实际开发中，面对的可能是数据规模小的数字

• 比较次数和移动（或交换）次数

  基于比较的排序算法，一种是元素比较大小，一种是元素交换或者移动

排序算法的内存消耗

• 算法的内存消耗通过空间复杂度衡量，排序算法也如此
• 原地排序算法：特指空间复杂度为 O(1)

排序算法的稳定性

凭借着执行效率和内存消耗衡量排序算法的好坏是不够的，还得看看算法的稳定性。简单来说，就是一组数组中相同的数字，在排序前和排序后的前后顺序是否改变，如果改变了，就是不稳定的，没改变，就是稳定的一个算法。

在实际开发中，我们要排序的不是整数，而是一组对象，要按照对象的某个 key 进行排序。

比如，现在给电商系统中的 “订单” 排序，订单有两个属性，订单时间，金额。
金额从小到大进行排序，对于金额相同的订单，按照订单时间从早到晚排序。

实现思想：借助稳定排序算法，先按照订单时间进行排序，排序完后使用稳定排序算法对金额进行排序。这样可以保证，相同的金额的订单保持着下单时间从早到晚的排序

常见的排序

• 冒泡排序、插入排序、选择排序【时间复杂度：O (n²)】
• 快速排序、归并排序 【时间复杂度：O(nlogn)】
• 桶排序、技术排序，基数排序 【时间复杂度 O(n)】

冒泡排序

• 冒泡排序只会操作相邻的两个数据

• 每次冒泡操作对相邻的两个元素进行比较，看是否满足大小关系要求

• 不满足就互换元素，每一次的冒泡至少有一个元素交换位置，重复 n 次，就完成了 n 个数据的排序工作。

• 比如：对 4，5，6，3，2，1 从小到大进行排序。

  冒泡操作的详细过程：

  

  代码实现：

  public class BubbleSortOne {
      public static void main(String[] args) throws Exception {
          int[] ints = {4,5,6,3,2,1};
          int[] ints1 = bubbleSort(ints, ints.length);
          System.out.println(Arrays.toString(ints1));
      }
  
      //冒泡排序，a 表示数组，n 表示数组大小
      public static int[] bubbleSort(int[] a, int n){
          int[] arr = Arrays.copyOf(a,n);
          if (n <= 1) {
              return null;
          }
          for (int i = 0; i < n; i++) {
              //设置一个何时终止冒泡的值
              boolean flag = false;
              for (int j = 0; j < n - 1; j++) {
                  if (arr[j] > arr[j+1]){
                      int temp = arr[j];
                      arr[j] = arr[j+1];
                      arr[j+1] = temp;
                      flag = true;
                  }
              }
              //跳出循环的条件
              if (!flag){
                  break;
              }
          }
          return arr;
      }
  }

  分析冒泡排序：

  • 冒泡排序涉及相邻数据交换，使用了常量级的临时空间，空间复杂度为 O（1），所以是一个原地排序的算法

  • 冒泡排序面对相同的两个元素时，不会交换，在排序前和排序后，相同的两个元素前后位置没有发生改变，所以是稳定的排序算法

  • 时间复杂度：

    最好的时间复杂度为 O(n)。比如：1，2，3，4，5，6，一次冒泡排序即可。

    最坏的时间复杂度为 O(n²)。比如：6，5，4，3，2，1，要进行 n 次的冒泡排序

  • 平均复杂度的分析：平均复杂度就是加权平均期望时间复杂度，结合概率论的知识分析对于冒泡排序会比较复杂。

  • 通过 “有序度“ 和 “逆序度”分析：

    有序元素对：a[i] <= a[j]，如果 i < j

    对于一个倒序的数组，比如：6,5,4,3,2,1 有序度为：0

    对于完全有序的数组，比如：1,2,3,4,5,6

    有序度为：n*(n-1)/2，就是15，这种完全有序的数组的有序度叫做满有序度

  • 逆序度的定义正好跟有序度相反（默认从小到大）

    逆序度 = 满有序度 - 有序度

    比如：要排序的数组的初始状态是：4,5,6,3,2,1。

    其中，有序元素队有（4,5），（4，6），（5，6）

    有序度为3。n =6，排序完成后终态的满有序度：n*(n-1)/2 = 15

    

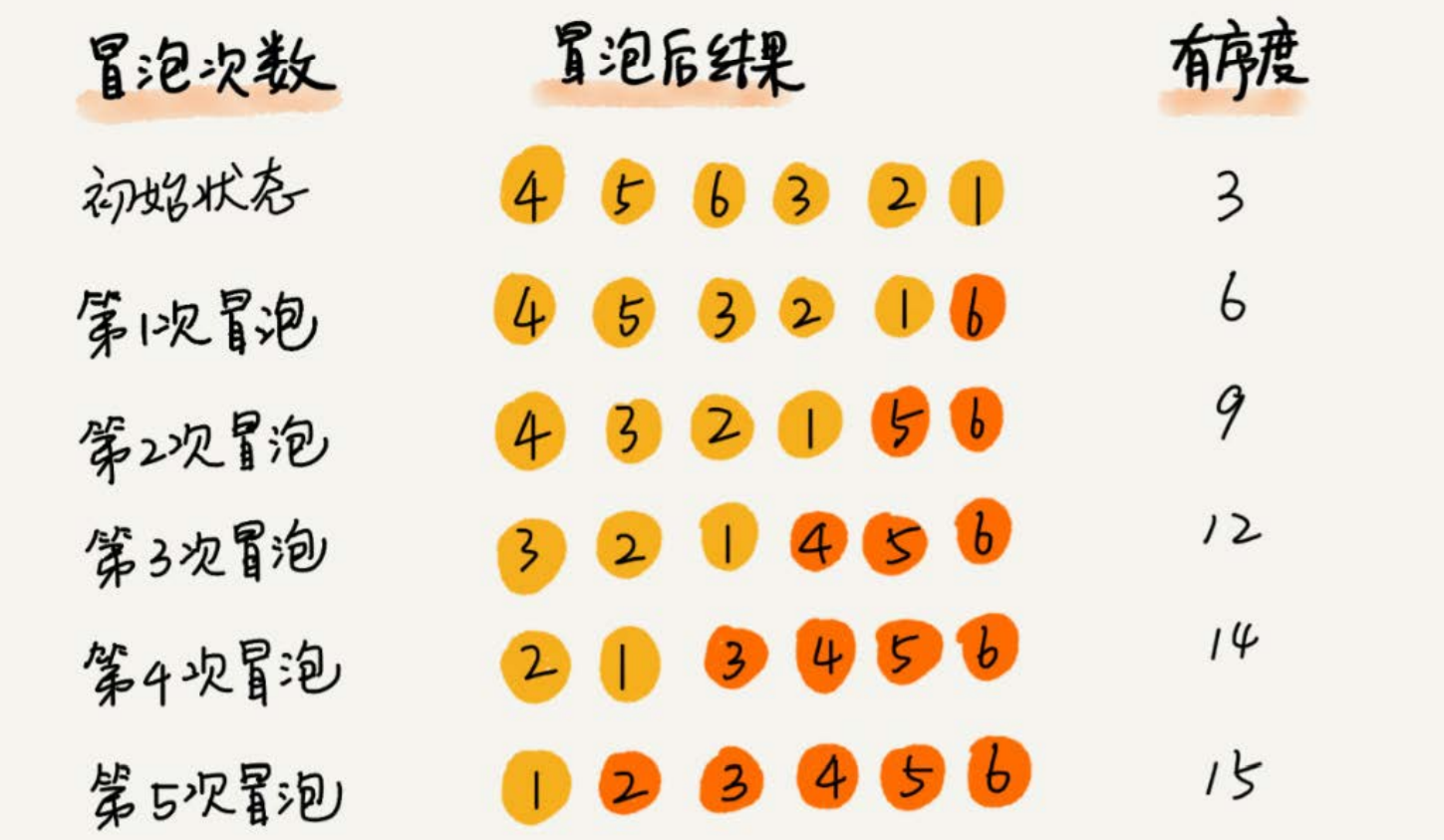
  • 冒泡排序包含两个操作原子，比较和交换。交换一次，有序度加一。交换的次数是确定的，n*(n-1)/2 - 初始有序度，15 - 3 = 12

    对于包含 n 个数据的数组进行冒泡排序，平均交换次数是多少呢？最坏情况下，初始状态的有序度为 0 ，要进行 n(n-1)/2次交换。最好情况下，初始状态的有序度为 n(n-1)/2，不需要。

    中间值为：n*(n-1)/4，平均情况下，需要继续n(n-1)/4次交换操作，比较操作比交换操作多，复杂度上次为 O(n²)，平均情况下的时间复杂度为O(n²)。

插入排序

• 要向一组有序的数组里，插入一个数据，如何做？

  遍历整个数组，找到这个数相应位置，进行插入

• 动态排序：动态地往有序集合中添加数组，通过这种方法保持集合中的数据有序。

• 插入排序如何借助动态排序思想实现排序：

  首先，将数据中的数据分为两个区间，已排序区间和未排序区间。初始已排序区间只有一个元素，是数组的第一个元素。

• 插入算法核心：将未排序区间中的元素，在已排序区间中找到合适的位置插入位置将其插入，并保证已排序区间数据一直有序。

  

• 插入排序包含两种操作：

  元素比较：我们将一个数据 a 插入已排序区间时，要将 a 与已排序区间的元素比较大小，找到合适的插入位置后，就进行元素移动

  元素移动：将插入点之后的元素都往后面移动一位

  对于从头到尾，从尾到头，元素的比较次数是有区别的，但是移动次数总是固定的，就等于逆序度

  

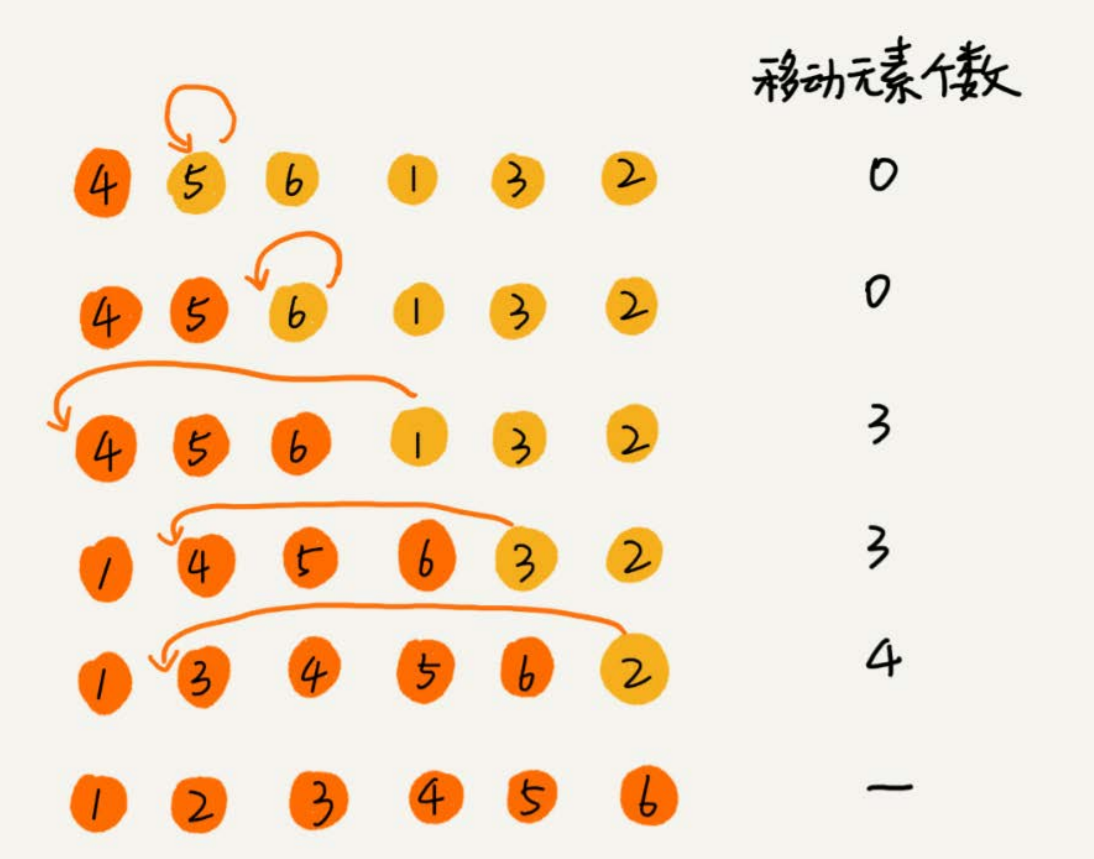
  满有序度：n(n-1)/2 = 15 ，初始有序度是5，逆序度为10

  移动个数总和为 3 + 3 + 4 = 10 = 逆序度

      // a 表示数组，n 表示数组大小
      public void insertionSort(int[] a,int n){
          if (n <= 1){
              return;
          }
          for (int i = 1; i < n; i++) {
              int value = a[i];
              int j = i - 1;
              //查找插入的位置
              for (;j >= 0; --j){
                  if (a[j] > value){
                      //数据移动
                      a[j+1] = a[j];
                  }else {
                      break;
                  }
              }
              //插入数据
              a[j+1] = value;
          }
      }

  • 插入算法是原地排序算法

    插入排序算法不需要额外的存储空间，空间复杂度为 O(1)

  • 插入排序是稳定的排序算法

    对于值相同的元素，后出现的那些值相同的元素排序后，插入到前面值相同的元素的后面，排序前后的原有的前后顺序不变

  • 插入排序的时间复杂度

    最好时间复杂度：如果排序的数据是有序的，并不需要搬移数据。假如从尾部到头部在有序数据中插入位置，只需要比较一个数据即可，这种情况下最好的时间复杂度为O(n)

**最坏时间复杂度：**如果数组是倒序的，每次插入都要在数组的第一个位置插入新的数据，也就是 O(n²)


  **平均时间复杂度：**在数组中，插入一个数据的平均复杂度为O(n)。插入排序中，需要进行 n 次的插入操作，平均复杂度为 O(n²)

选择排序

• 每次会从未排序区间中找到最小的元素放到已排序区间的末尾

  

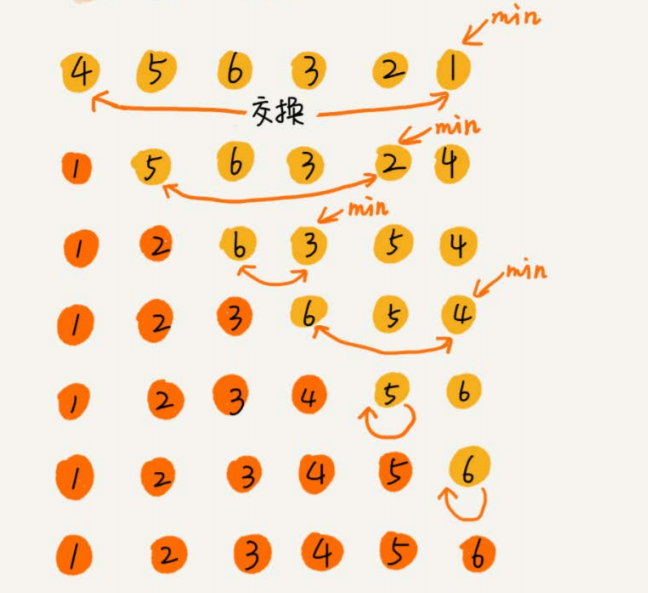
• 空间复杂度为 O(1)，是原地排序算法。最好、最坏、平均状况时间复杂度为O(n²)

• 不是稳定的排序算法，因为每次排序找的是最小值，并且和前面的元素交换了位置，破坏了稳定性

  比如：1，2，1，0，5，第一次找到最小元素0，与第一个元素交换位置，数组中两个 “1” 的前后顺序就变了，不稳定排序算法

插入排序比冒泡排序受欢迎的缘由

• 相同点：冒泡排序和插入排序的时间复杂度都是 O(n²)，都是原地排序算法；不管怎么优化，元素的移动次数都是等于原始数据的逆序度

• 不同点：代码实现方面，冒牌排序进行的数据交换要比插入排序更为复杂，冒泡排序需要进行三个赋值操作，而插入排序只需要进行一个赋值操作即可

  //冒泡排序中数据的交换操作：
  if (a[j] > a[j+1]) { // 交换
   int tmp = a[j];
   a[j] = a[j+1];
   a[j+1] = tmp;
   flag = true;
  }
  //插入排序中数据的移动操作：
  if (a[j] > value) {
   a[j+1] = a[j]; // 数据移动
  } else {
   break;
  }

• 如果把执行一个赋值语句记为单位时间，分别用冒泡排序和插入排序对同一个逆序度为 K 的数组进行排序

  冒泡排序：需要进行 K 次操作，一次操作要执行三个赋值语句，交换总耗时为：3 * K

  插入排序：需要进行 K 次操作，一次操作执行一个数据移动语句，交换总耗时： K

  	是否原地排序	是否稳定	最好	最坏	平均
  冒泡排序	√	√	O(n)	O(n²)	O(n²)
  插入排序	√	√	O(n)	O(n²)	O(n²)
  选择排序	√	×	O(n²)	O(n²)	O(n²)

归并排序

• 归并排序的核心思想：要排序一个数组，我们把数组从中间分成前后部分，然后对前后两部分分别排序 ，再把排序好的两部分合并在一起，数组就有序了。

• 归并排序使用的是分治思想，把大问题分成小问题，小问题解决了，大问题也就解决了，而分治算法一般都是用递归实现的，分治是一种解决问题的处理思想，递归是一种编程技巧。

• 递归的步骤：

  • 分析递推公式
  • 找到终止条件
  • 将递推公式翻译成递归代码

• 归并排序的递推公式：

  merge_sort(p..r) = merge(merge_sort(p..q) ,merge_sort(q+1…r))

  merge_sort(p..r)表示，将下标从 p 到 r 的数组进行排序，将排序问题转化成了两个子问题，merge_sort(p..q), merge_sort(q+1…r))。其中下标 q 等于 p 和 r 的中间位置，也就是(p+r)/2。当下标从 p 到 q 和从 q+1 到 r 这两个子数组都排序之后，再合并两个子数组，那么 p 到 r 的数据也就排序完了。

  归并排序的终止条件：

  p >= r

  伪代码：

  // 归并排序算法, A是数组，n表示数组大小
  merge_sort(A, n) {
   merge_sort_c(A, 0, n-1)
  }
  // 递归调用函数
  merge_sort_c(A, p, r) {
   // 递归终止条件
   if p >= r then return
   // 取p到r之间的中间位置q
   q = (p+r) / 2
   // 分治递归
   merge_sort_c(A, p, q)
   merge_sort_c(A, q+1, r)
   // 将A[p...q]和A[q+1...r]合并为A[p...r]
    merge(A[p...r], A[p...q], A[q+1...r])

  merge(A[p…r], A[p…q], A[q+1…r]) 这个函数的作用就是，将已经有序的A[p…q]和A[q+1…r] 合并成一个有序的数组，并且放入 A[p…r]

过程图解：

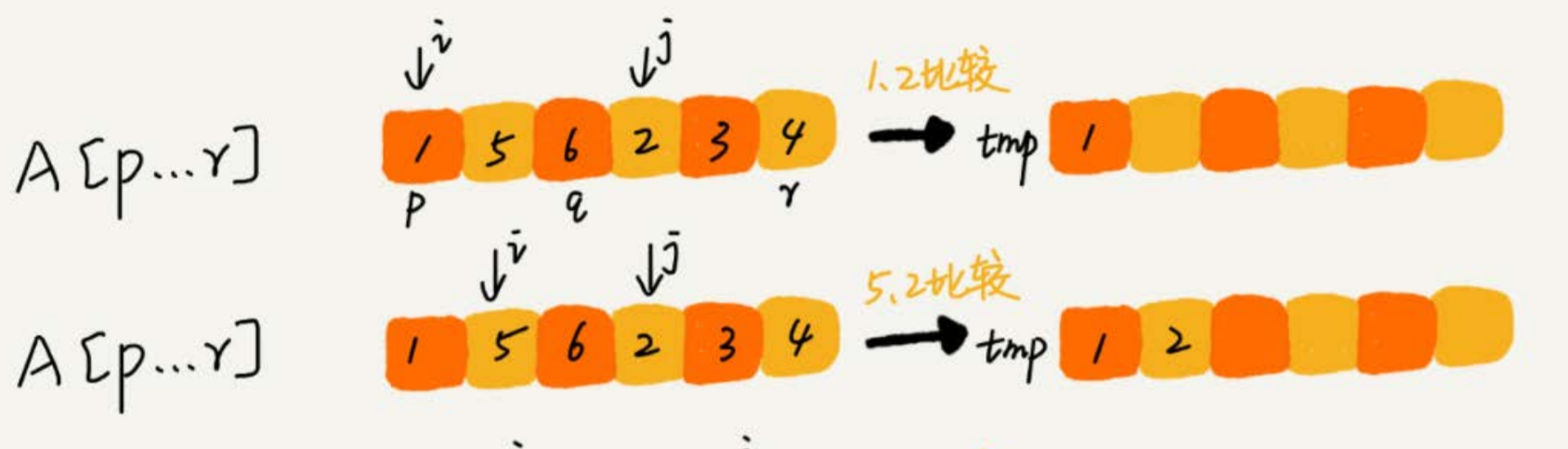
申请一个临时数组，大小与 A[p..r] 相同。我们用两个游标 i 和 j ，分别指向 A[p..q] 和 A[q+1..r]的第一个元素。比较这个两个元素 A[i] 和 A[j] ，如果 A[i ] <= A[j]，放进临时数组 tmp，i 后移一位，否则 A[j] 放入数组 tmp， j 后移一位。

继续上述比较过程，直到其中一个子数组中的所有数据都放入临时数组中，再把另一个数组中的数据依次加入到临时数组的末尾

最终将临时数组 tmp 的数据拷贝到原数据 A[p..r] 中

代码的实现：

   public static void main(String[] args) {
          int[] arr = {11,8,3,7,9,2,1,5};
          //新建临时数组进行存放
          int[] tmp = new int[arr.length];
          mergeSort(arr,0,arr.length-1,tmp);
          for (int i = 0; i < arr.length; i++) {
              System.out.println(arr[i] + "");
          }
      }

      /**
        * 
        * @param arr 原始数组
        * @param low 第一个元素
        * @param mid 中间元素
        * @param high 最后一个元素
        * @param tmp 临时数组
        * @Return void
        * @author XiaoXin
        * @date 2020/5/9 15:10 
        */
      public static void merge(int[] arr,int low,int mid,int high,int[] tmp){
          int i = 0;
          //左边序列
          int j = low;
          //右边序列起始索引
          int k = mid + 1;
          while (j <= mid && k <= high){
              //
              if (arr[j] < arr[k]){
                  tmp[i++] = arr[j++];
              }else {
                  tmp[i++] = arr[k++];
              }
          }
          //如果左边还有剩余，则将其全部拷贝进 tmp[] 中
          while (j <= mid){
              tmp[i++] = arr[j++];
          }

          //如果右边还有剩余，则将其全部拷贝进 tmp[] 中
          while (k <= high){
              tmp[i++] = arr[k++];
          }

          //将 tmp 中的数组拷贝回原数组中
          for (int t = 0; t < i; t++){
              arr[low + t] = tmp[t];
          }
      }

      private static void mergeSort(int[] arr, int low, int high, int[] tmp) {
          if (low < high){
              int mid = (low + high) / 2;
              //对左边索引进行排序
              mergeSort(arr,low,mid,tmp);
              //对右边索引进行排序
              mergeSort(arr,mid+1,high,tmp);
              //合并索引
              merge(arr,low,mid,high,tmp);
          }
      }

• 归并排序的性能分析：

  一、是不是稳定的排序算法？

  主要看的是 merge() 函数，也就是两个有序子数组合并成一个有序数组的部分代码，合并过程中，如果 A[p..q] 和 A[q+1,r] 之间有相同元素，先把 A[p..q] 的元素放入 tmp 数组，这样相同的元素在合并前后的先后顺序不变。所以，它是一个稳定的排序算法

二、归并排序的时间复杂度

前面有提到归并排序，分治思想，其实也就是递归嘛。如何分析递归的时间复杂度

递归的使用场景：问题 a 能分解成多个子问题 b 、c ，那求解问题 a 就可以分解为求解问题 b 、c 。问题 b 、 c 解决后，将 b 、c 的结果合并成 a 的结果

假如定义求解问题 a 的时间是 T(a)，求解问题 b 、c 的时间分别为 T(b) 和 T(c)，即是：T(a) = T(b) + T(c) + K

其中 K 等于将两个子问题 b 、c 的结果合并成问题 a 的结果所消耗的时间

将归并排序套入其中

假设对 n 个元素进行归并排序所需要的时间为 T(n) ，分解成左右索引进行排序的时间为 T(2/n)。merge() 函数合并两个有序子数组的时间复杂度为 O(n).

归并排序的时间复杂度的计算公式就是：

T(1) = C; n=1 需要常量级的执行时间，为 C

T(n) = 2*T(2/n) + n; n>1

  T(n) = 2*T(n/2) + n
   = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
   = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
   = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
   ......
   = 2^k * T(n/2^k) + k * n

当 T(n/2^k)=T(1) 时，也就是 n/2^k=1，我们得到 k=log2n 。

K代入上面的公式，T(n) = Cn + nlog2n (2是小2，log2n)

T(n)就等于O(nlogn)。所以归并排序的时间复杂度是O(nlogn)。

归并排序的执行效率与数组是否有序无关，所以最好、最坏、平均情况，复杂度都是O(nlogn)。

三、归并排序的空间复杂度

由于在合并两个有序数组为一个有序数组的时候，需要借助额外的存储空间，因此归并排序并不是一个原地排序算法。

在申请额外的存储空间时，因为只是临时的，所以在合并后，这个临时空间就被释放。从 CPU 的角度来说，任意时刻，只有一个函数在运行，只会有一个临时空间在使用。临时空间也不会超过 n 个数据的大小。空间复杂度为 O(n)

快速排序

• 快排使用的也是分治思想。

• 快速排序的思想：假如给定一组 a 到 c 的数据，对它们进行排序，我们首先要找到 a 到 c 中任意一个数据作为 pivot (节点)，把小于 pivot 的放到左边去，把大于 pivot 的放到右边去，pivot 放在中间。这样就可以分成了三个区域，a 到 b-1 之间为小于 pivot 的，pivot 为一个区域，b + 1 到 c 之间为大于 pivot 的

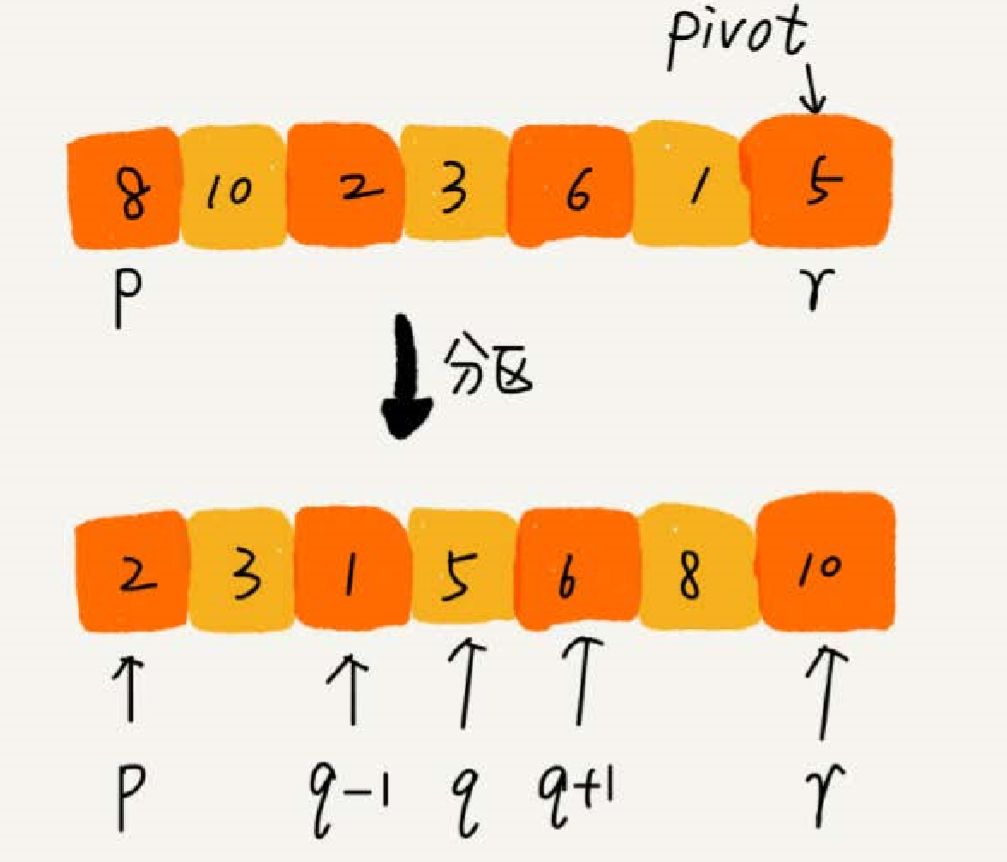
• 根据分治，递归的思想，先用递归排序，如图，我们可以用递归排序下标从 p 到 q - 1 的数据和下标从 q + 1 到 r 之间的数据，直到区间缩小为 1 ，说明数据有序。

• 递推公式：

  quick_sort(p..r) = quick_sork(p..q-1) + quick_sork(q+1..r)

• 终止条件：

  p >= r

  转换成伪代码实现

           // 快速排序，A是数组，n表示数组的大小
          quick_sort(A, n) {
              quick_sort_c(A, 0, n-1)
          }
          // 快速排序递归函数，p,r为下标
          quick_sort_c(A, p, r) {
              if p >= r then return 
              q = partition(A, p, r) // 获取分区点
              quick_sort_c(A, p, q-1)
              quick_sort_c(A, q+1, r)
          }

  归并排序中有一个 merge() 合并函数，快排用的是 partition() 分区函数。

  partition() 分区函数的作用是随机选择一个元素作为 pivot （一般情况下，选择 p 到 r 区间的最后一个元素），之后对 A[p..r] 分区，函数返回 pivot 下标

  不考虑空间消耗的话，partition() 分区函数可以申请两个临时空间，遍历 A[p..r]，将比 pivot 小的放临时数组 X ，将比 pivot 大的放临时数组 Y，最后合并 X 和 Y 数组复制到 A[p..r]

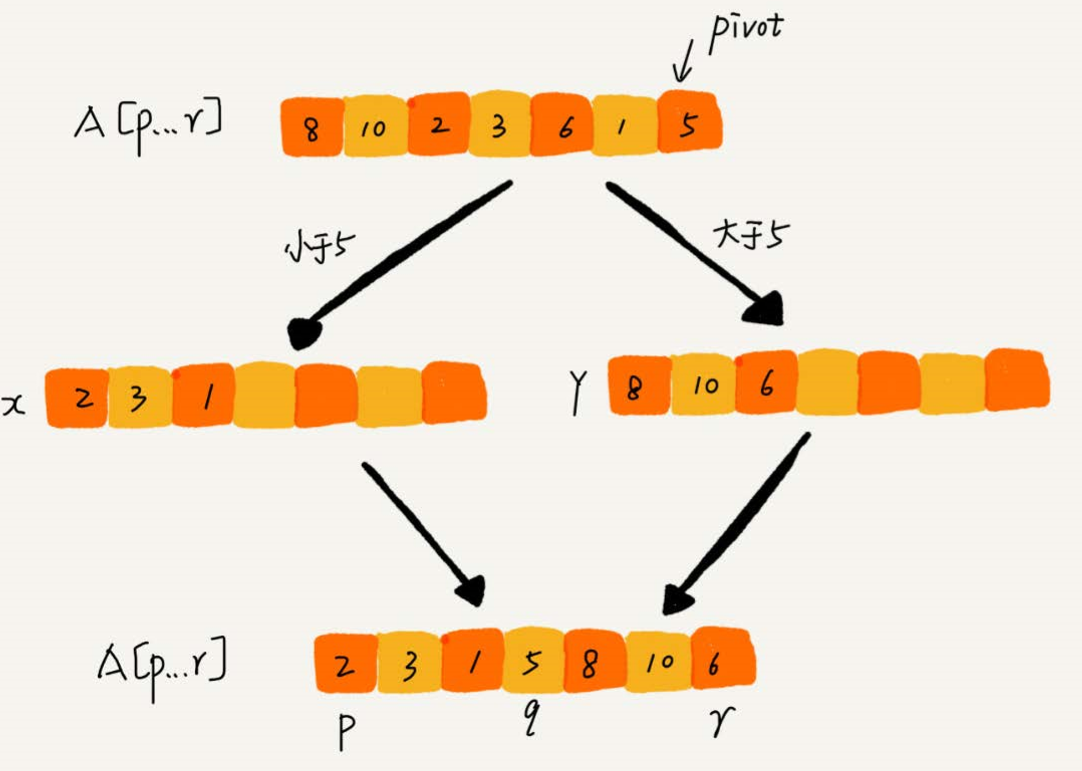
这样一来，partition() 函数需要很多额外空间，所以快排就不为原地排序算法。

• 将快排优化成原地排序算法的话，空间复杂度要为 O(1)，partition（）分区函数不能拥有额外空间，需要在 A[p..r] 里完成分区的操作

  伪代码：

          partition(A, p, r) {
              pivot := A[r]
              i := p
              for j := p to r-1 do {
                  if A[j] < pivot {
                      swap A[i] with A[j]
                      i := i+1
                  }
              }
              swap A[i] with A[r]
              return i

  类似于选择排序，我们通过游标 i 将 A[p..r-1] 分成两部分，A [p..i-1] 的元素小于 pivot （已处理区间），A[i..r-1] （未处理区间）。从未处理区间中取元素 A[j] 与 pivot 比较，假如小于 pivot ，就放到已处理区间的后面，即为 A[i]。

  交换：在 O(1) 的时间复杂度内完成插入操作，将 A[i] 和 A[j] 交换，就可以在 O(1) 时间复杂度内将 A[j] 放到下标为 i 的位置

  

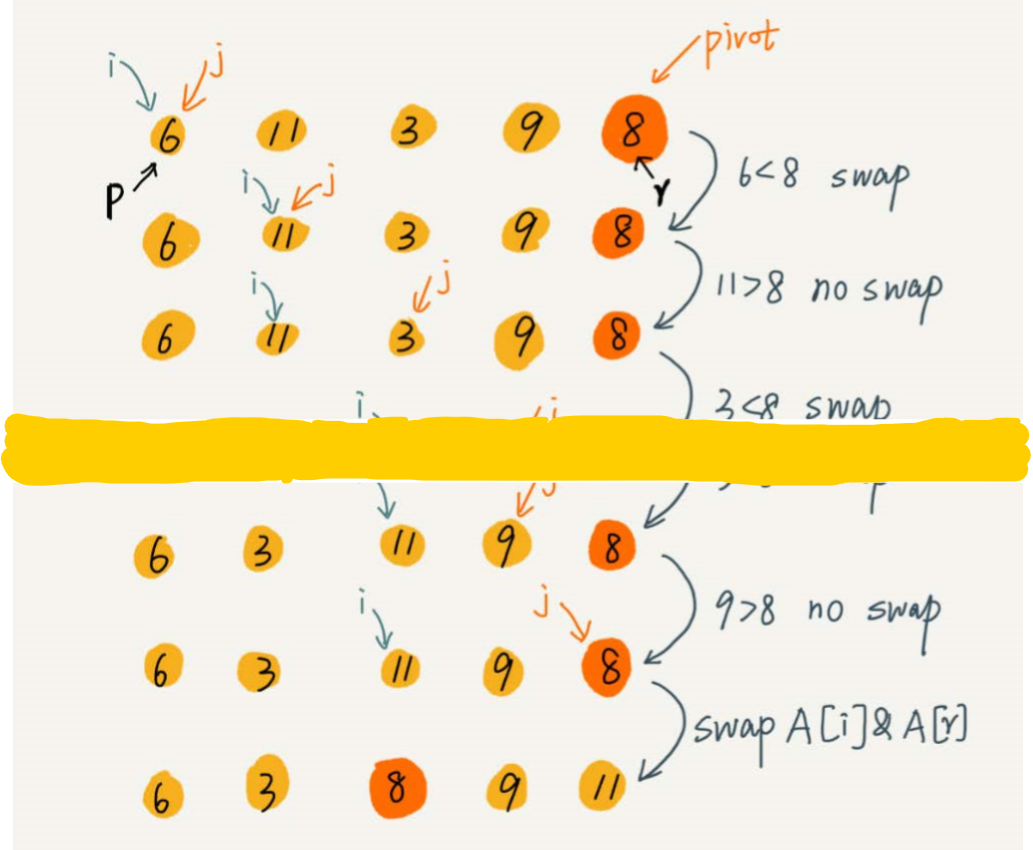
  由于涉及到交换，在第一次分区操作后，相同的数字交换后，会改变先后顺序的位置，它不是一个稳定的排序算法

• 归并排序与快速排序的区别：

  

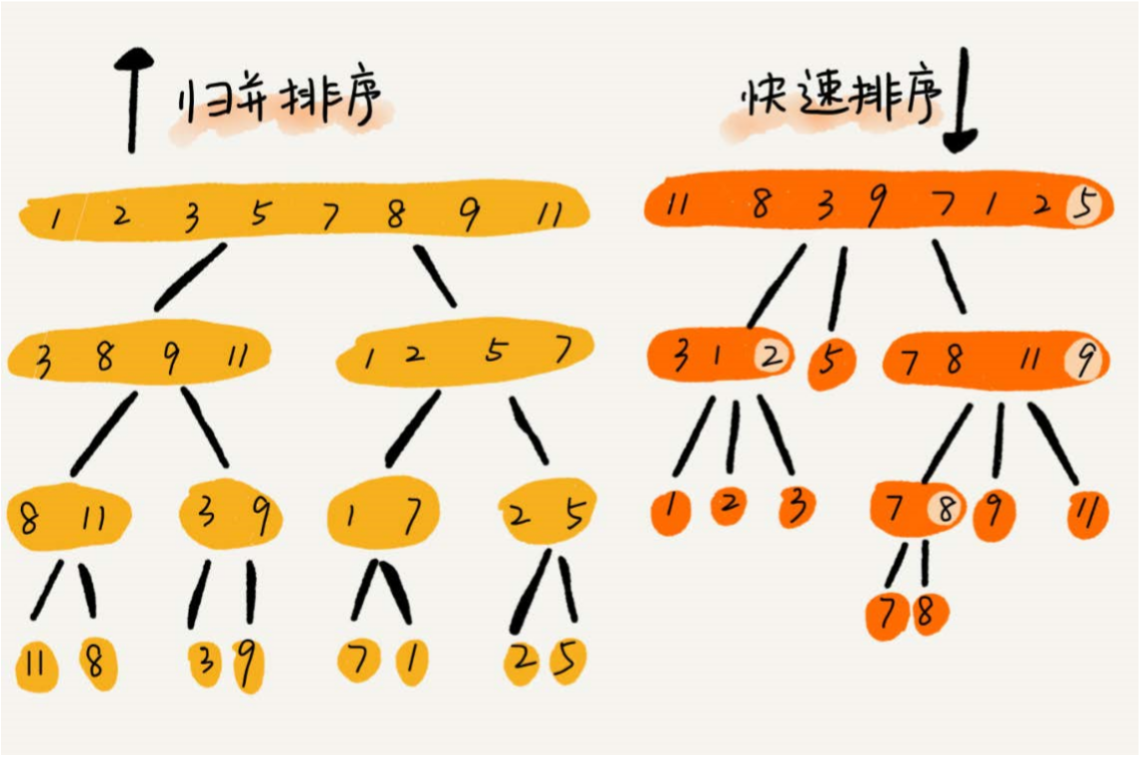
	归并排序	快速排序
相同	思想：都用到了分治思想，
不同	处理过程：由上到下，先处理子问题，再合并 稳定、非原地排序算法	处理过程：由下到上，先分区，再处理子问题 不稳定，原地排序算法

快排的时间复杂度：

最好时间复杂度：O(nlogn) 对应的情况：如果每次刚好能将分区分成两个大小相同的区间，快排的时间复杂度于递推求解公式和归并排序是一致的

最坏时间复杂度：O(n²) ，假如给定的数组是排序好的，每次选择最后一个元素作为 pivot ，每次分区得到的两个区间都是不同的，大约要进行 n 次分区，才能完成整个操作，每次分区平均要扫描 n/2 个元素，时间复杂度就从 O(nlogn) 退化成了 O(n²)

平均复杂度：T(n)在大部分情况下的时间复杂度都可以做到O(nlogn)，只有在极端情况下，才会退化到O(n2)。

实现代码：

 public static void quickSort(int[] arr,int low,int high){
        int i,j,temp,t;
        if(low > high){
            return;
        }
        i = low;
        j = high;
        //temp就是基准位
        temp = arr[low];

        while (i<j) {
            //先看右边，依次往左递减
            while (temp  <= arr[j] && i<j) {
                j--;
            }
            //再看左边，依次往右递增
            while (temp >= arr[i]&&i<j) {
                i++;
            }
            //如果满足条件则交换
            if (i<j) {
                t = arr[j];
                arr[j] = arr[i];
                arr[i] = t;
            }

        }


    }


    public static void main(String[] args){
        int[] arr = {10,7,2,4,7,62,3,4,2,1,8,9,19};
        quickSort(arr, 0, arr.length-1);
        for (int i = 0; i < arr.length; i++) {
            System.out.println(arr[i]);
        }
    }

桶排序

• 实现思想：将排序的数据放在几个有序的桶里，每个桶对桶里的数据进行排序，排序好之后，依次从每个桶里取出数据，就实现了有序

• 时间复杂度为：O（n）

  假如要排序的数据有 n 个，把他们均匀的分在 m 个桶里，那么每个桶中就有k= n/m 个数据，每个桶里使用快速排序，时间复杂度就为 O(klognk)。m 个桶排序时，就是 O(m * k * logk)，k = n/m，O(n * log(n/m))，如果数据 n 等于桶的个数 m ，那么 log(n/m) 是一个非常小的常量，桶排序的复杂度接近 O(n)。

• 最坏情况时间复杂度：O(n * logn)

  把全部数据都放在一个桶里的情况

• 桶排序适用于外部排序，外部排序是数据存储在外部磁盘中，数据量大，内存有限，无法加载到内存中

• 实现代码：

  import java.util.ArrayList;
  import java.util.LinkedList;
  import java.util.List;
  import java.util.ListIterator;
  
  public class Main {
  
      public static void main(String[] args) {
          // 输入元素均在 [0, 10) 这个区间内
          float[] arr = new float[] { 0.12f, 2.2f, 8.8f, 7.6f, 7.2f, 6.3f, 9.0f, 1.6f, 5.6f, 2.4f };
          bucketSort(arr);
          printArray(arr);
      }
  
      public static void bucketSort(float[] arr) {
          // 新建一个桶的集合
          ArrayList<LinkedList<Float>> buckets = new ArrayList<LinkedList<Float>>();
          for (int i = 0; i < 10; i++) {
              // 新建一个桶，并将其添加到桶的集合中去。
              // 由于桶内元素会频繁的插入，所以选择 LinkedList 作为桶的数据结构
              buckets.add(new LinkedList<Float>());
          }
          // 将输入数据全部放入桶中并完成排序
          for (float data : arr) {
              int index = getBucketIndex(data);
              insertSort(buckets.get(index), data);
          }
          // 将桶中元素全部取出来并放入 arr 中输出
          int index = 0;
          for (LinkedList<Float> bucket : buckets) {
              for (Float data : bucket) {
                  arr[index++] = data;
              }
          }
      }
  
      /**
       * 计算得到输入元素应该放到哪个桶内
       */
      public static int getBucketIndex(float data) {
          // 这里例子写的比较简单，仅使用浮点数的整数部分作为其桶的索引值
          // 实际开发中需要根据场景具体设计
          return (int) data;
      }
  
      /**
       * 我们选择插入排序作为桶内元素排序的方法 每当有一个新元素到来时，我们都调用该方法将其插入到恰当的位置
       */
      public static void insertSort(List<Float> bucket, float data) {
          ListIterator<Float> it = bucket.listIterator();
          boolean insertFlag = true;
          while (it.hasNext()) {
              if (data <= it.next()) {
                  it.previous(); // 把迭代器的位置偏移回上一个位置
                  it.add(data); // 把数据插入到迭代器的当前位置
                  insertFlag = false;
                  break;
              }
          }
          if (insertFlag) {
              bucket.add(data); // 否则把数据插入到链表末端
          }
      }
  
      public static void printArray(float[] arr) {
          for (int i = 0; i < arr.length; i++) {
              System.out.print(arr[i] + ", ");
          }
          System.out.println();
      }
  
  }

计数排序

• 计数排序是桶排序的一种特殊情况，吐过要排序 n 个数据，范围不大时，比如最大值为 K ，

  把数据划分为 k 个桶，每个桶内的数据相同，省掉了桶内排序时间。

  其实高考分数排序，也是这个道理，假如有 50W 考生，要对他们的分数进行排序。

  首先，高考最低分为 0 分，最高分为 900 分，就可以分成 901 个桶，每个桶内装的都是分数一样的考生。

  就不需要再次进行排序，只要遍历整个桶，将桶内考生输出到数组中，便可实现排序，时间复杂度为 O（n）

• 计数排序的实现：

  • 假如只有 8 个考生，分数在 0 - 5 分之间。

  • 这 8 个考生的成绩放在一个数组 A[8] 中，分别为

    2，5 ，3，0，2，3，0，3

  • 设立一个大小为 6 的数组 C[6] 表示桶，下标对应的是分数，存储的是考生的个数

  遍历考生分数即可

  

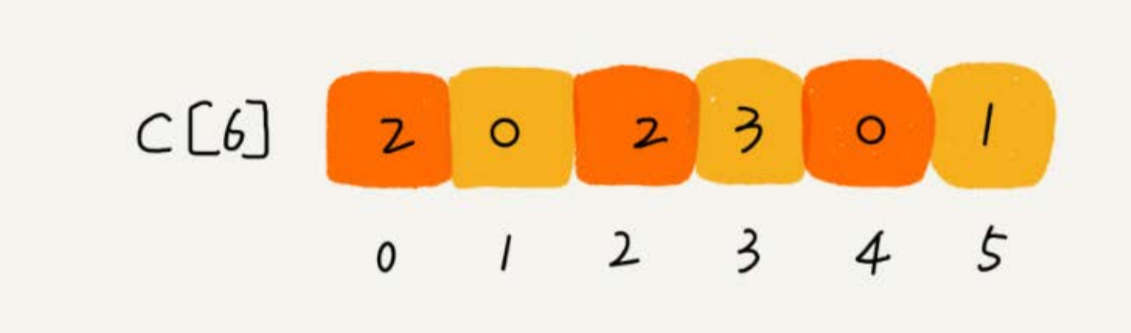
分数小于 3 分的有 3 个，等于 3 分的有 3 个，那么在排序后的 A【8】 数组里，分数为 3 的占据的下标为4，5，6

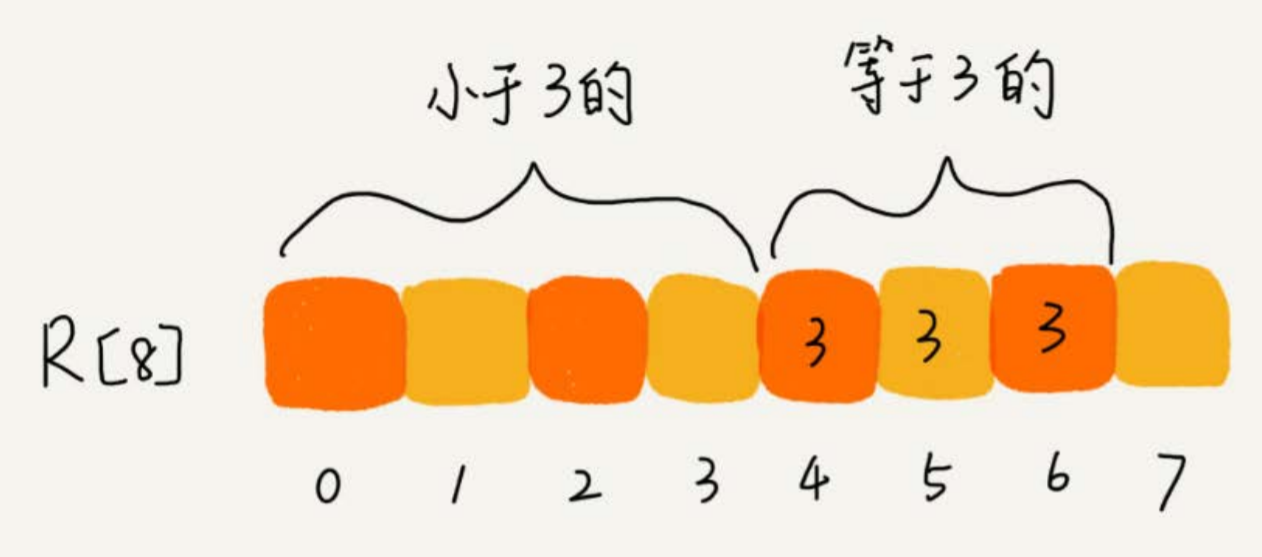
• 计算每个考生在有序数组中对应的位置

  C【K】存储的是小于等于分数 K 的人数

  

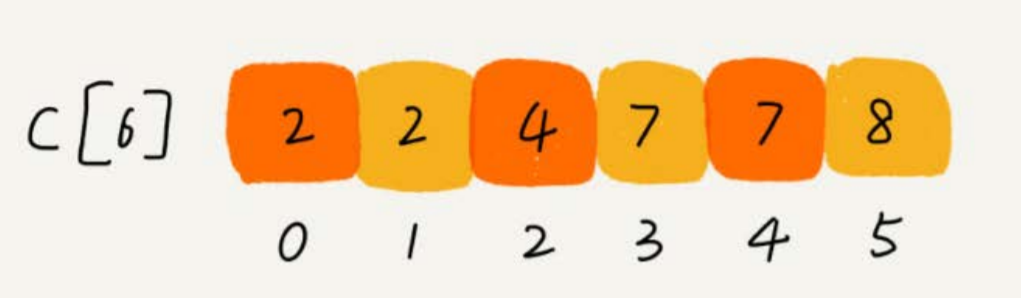
  • 从后往前进行遍历 C【6】数组，扫描到 3 时，从数组中取出下标为 3 的数值 7 ， 数组 C 会发生改变，本来分数小于等于 3 的考生有 7 个，取出一个 3 之后，那么 C【3】的值要减去 1 ，变成 6 。

  ​

  ​

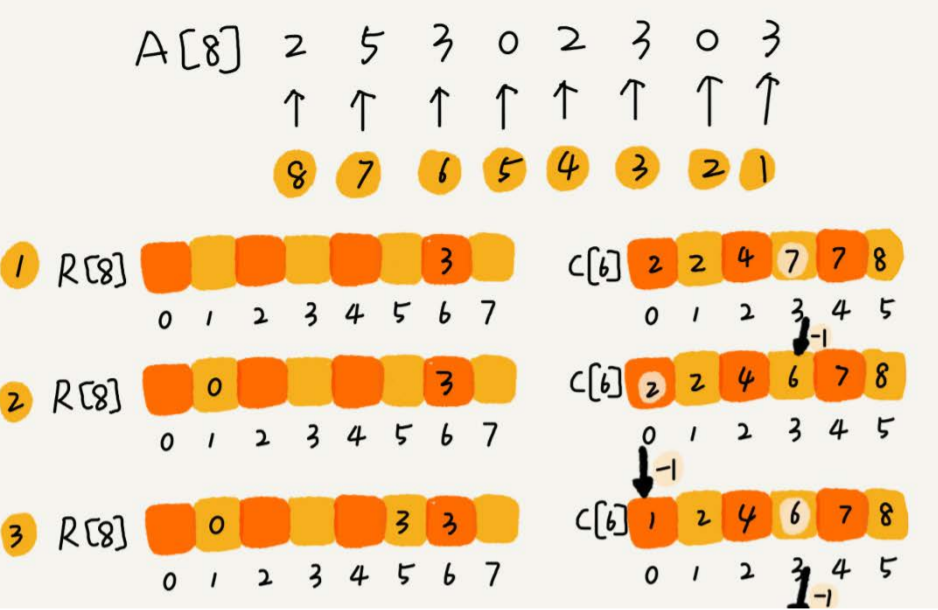
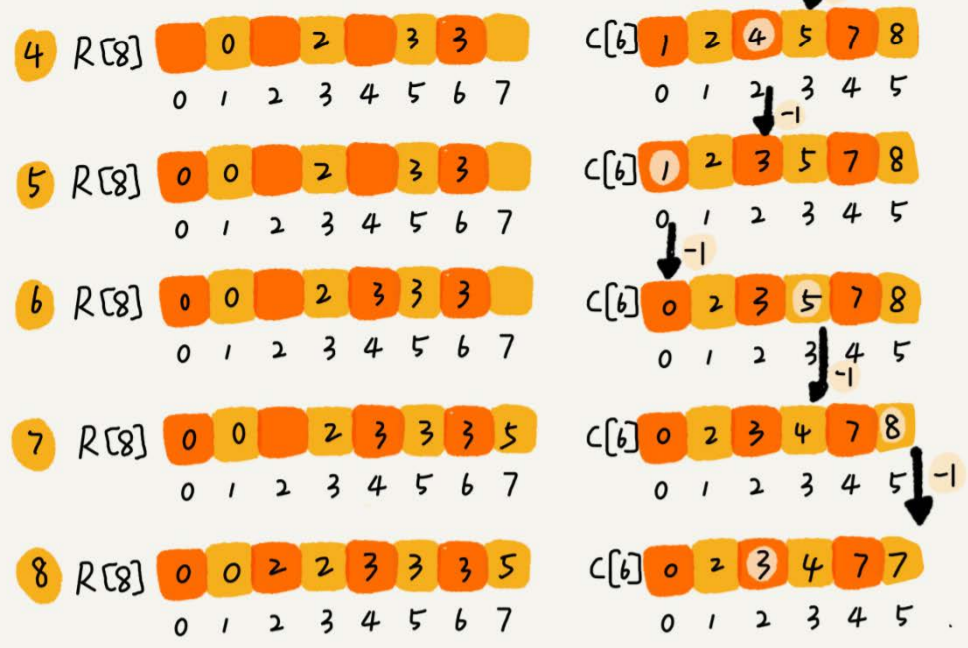
• 代码实现

  // 计数排序，a是数组，n是数组大小。假设数组中存储的都是非负整数。
      public void countingSort(int[] a, int n) {
          if (n <= 1)
              return;
          // 查找数组中数据的范围
          int max = a[0];
          for (int i = 1; i < n; ++i) {
              if (max < a[i]) {
                  max = a[i];
              }
          }
          // 申请一个计数数组c，下标大小[0,max]
          int[] c = new int[max + 1];
          for (int i = 0; i <= max; ++i) {
              c[i] = 0;
          }
          // 计算每个元素的个数，放入c中
          for (int i = 0; i < n; ++i) {
              c[a[i]]++;
          }
          // 依次累加
          for (int i = 1; i <= max; ++i) {
              c[i] = c[i-1] + c[i];
          }
          // 临时数组r，存储排序之后的结果
          int[] r = new int[n];
          // 计算排序的关键步骤，有点难理解
          for (int i = n - 1; i >= 0; --i) {
              int index = c[a[i]]-1;
              r[index] = a[i];
              c[a[i]]--;
          }
          // 将结果拷贝给a数组
          for (int i = 0; i < n; ++i) {
              a[i] = r[i];
          }
      }

• 这种方法是利用了另外一个数组来进行计数。

• 计数排序适用的范围只能是数据范围不大的场景，比如：数据范围 a 比要排序的数据 b 要大很多，就不适合采用计数排序的方法。

• 计数排序只能适用于非负整数进行排序，如果排序的数据是其他类型的，要在不改变相对大小的去情况下，转化成非负数。比如：排序的数据中有负数，数据范围是【-1000，1000】，排序前需要对每个数据加 1000 ，转换成非负数

基数排序

• 基数排序就是将待排序数据拆分成多个关键字进行排序，本质是关键字排序

  多关键字排序时有两种解决方案：

  最高位优先法

  最低位优先法

  例如，对以下数据序列进行排序

  192，221，12，23

  数据最多只有 3 位，可以拆分成 3 个关键字：百位（百位）、十位、个位（低位）

• 按照习惯思维，会先比较百位，百位大的数据大，百位相同的再比较十位，十位的数据大，最后比较个位数

  但计算机按照人的思维，实现起来会有一定的困难，比较十位时，还得看看百位是否相同，增加难度，因此计算机采用最低位优先法

• 基数排序对子关键字进行排序时，得借助另一个稳定的算法

  PS：使用不稳定的排序算法，最后一次排序只会考虑最高位的大小关系，而不考虑其它位的大小关系，那么毫无意义

  子关键字位于 0 - 9 的这个范围，所以使用桶排序会很不错。

  代码实现：

   public static void main(String[] args) {
          int[] data = new int[] { 1100, 192, 221, 12, 23 };
          print(data);
          radixSort(data, 10, 4);
          System.out.println("排序后的数组：");
          print(data);
      }
  
      public static void radixSort(int[] data, int radix, int d) {
          // 缓存数组
          int[] tmp = new int[data.length];
          // buckets用于记录待排序元素的信息
          // buckets数组定义了max-min个桶
          int[] buckets = new int[radix];
  
          for (int i = 0, rate = 1; i < d; i++) {
  
              // 重置count数组，开始统计下一个关键字
              Arrays.fill(buckets, 0);
              // 将data中的元素完全复制到tmp数组中
              System.arraycopy(data, 0, tmp, 0, data.length);
  
              // 计算每个待排序数据的子关键字
              for (int j = 0; j < data.length; j++) {
                  int subKey = (tmp[j] / rate) % radix;
                  buckets[subKey]++;
              }
  
              for (int j = 1; j < radix; j++) {
                  buckets[j] = buckets[j] + buckets[j - 1];
              }
  
              // 按子关键字对指定的数据进行排序
              for (int m = data.length - 1; m >= 0; m--) {
                  int subKey = (tmp[m] / rate) % radix;
                  data[--buckets[subKey]] = tmp[m];
              }
              rate *= radix;
          }
  
      }
  
      public static void print(int[] data) {
          for (int i = 0; i < data.length; i++) {
              System.out.print(data[i] + "\t");
          }
          System.out.println();
      }
  

• 基数排序的时间复杂度为 O（n）

• 基数排序对排序的数据是有要求的，需要可以分割出独立的 “位” 来比较，而且位之间有递进的关系，如果 a 数据的高位比 b 数据大，剩下的低位就不需要比较了。每一位的数据范围不能过大，要能使用线性排序算法来排序，不然时间复杂度无法保持 O（n）

选择合适的排序方法

	时间复杂度	是否稳定排序	是否原地排序
冒泡排序	O（n²）	√	√
插入排序	O（n²）	√	√
选择排序	O（n²）	×	√
快速排序	O（nlogn）	×	√
归并排序	O（nlogn）	√	×
计数排序	O（n+k）k为数据范围	√	×
桶排序	O（n）	√	×
基数排序	O（dn）d是维度	√	×

线性排序算法的时间复杂度比较低，适用场景比较特殊。

如果写一个通用的排序函数，不能选择线性排序算法

• 对小规模的数据进行排序，可选择时间复杂度O（n²）的算法，
• 对大规模数据进行排序，时间复杂度为 O（nlogn）的算法更高效。
• 兼顾任意规模的数据进行排序，首选时间复杂度为 O（nlogn）的排序算法实现

二分查找法

二分查找法其实也叫折半查找算法，针对有序数据集合的查找算法。

二分思想无处不在

生活中的例子

有一个小游戏，就是你在 0- 99 的整数里面猜，你每说的一个数，我会告诉你这个数比正确答案大还是小，直到你猜中为止。

假如写的数字是 23 ，按照下图步骤试试，如果中间数有两个，那么取最小的那个

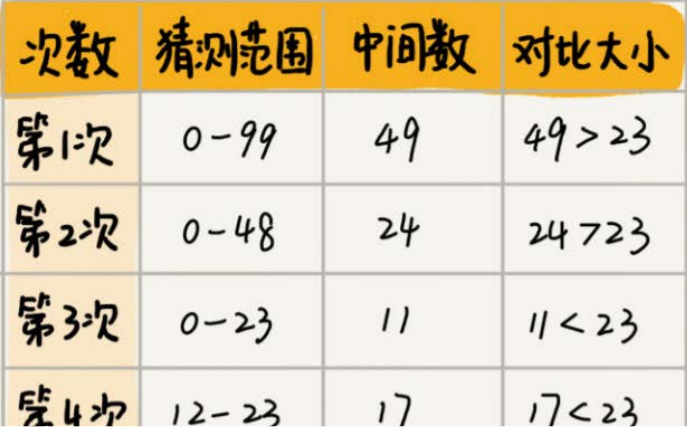
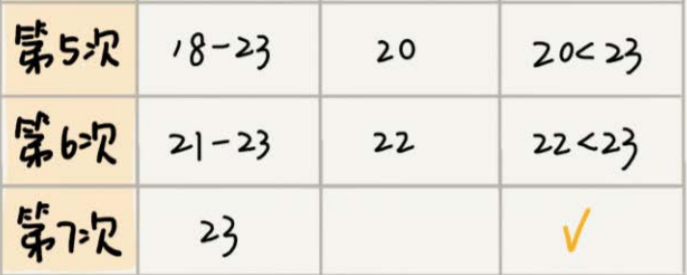
实际开发的例子

假设有 1000 条订单数据，已经按照订单金额从小到大排序，每个订单金额都不同，并且最小单位是 元。我们现在想知道是否存在金额等于 19 元的订单。如果存在，则返回订单数据，如果不存在则返回 null。

最简便的方法，可以遍历这 1000 条订单，找到等于 19 元的订单为止，查询效率比较低下，最坏情况下，可能要遍历 1000 条数据才能找到

使用二分查找法更快的解决。

假如只有 10 个订单，订单金额分别是：8，11，19，23，27，33，45，55，67，98

利用二分思想，每次都与区间的中间数据比较大小，缩小查找区间的范围。

low 和 high 表示待

参考文献：《极客时间》数据结构与算法之美 王争

To be completed…